Перетворення неоднорідних граничних умов в однорідні при використанні методу розділення перемінних
Вище було показано, що метод розділення перемінних є досить могутнім, а одержувані з його допомогою розв’язки представляються в зручній формі. Проте цей метод застосовний не до всіх задач. Для застосовності методу розділення перемінних граничні умови повинні бути лінійними й однорідними, тобто
Покажемо, яким чином задача з неоднорідними граничними умовами вигляду: рівняння теплопровідності
граничні умови
початкова умова
може бути вирішена шляхом зведення її до задачі з однорідними граничними умовами. Розглянемо найпростішу задачу про поширення тепла в теплоізольованому стержні, кінці якого підтримуються при постійних температурах Т1, Т2, тобто
Труднощі цієї задачі в тому, що, оскільки граничні умови в ній неоднорідні, ми не можемо вирішувати її методом розділення перемінних. Однак, мабуть, що при t ® ¥ розв’язок нашої задачі прагне до стаціонарного розв’язку, що лінійно змінюється (уздовж х) від температури Т1 до температури Т2 (Рис.3).
Іншими словами, розумно припустити, що температуру в нашій задачі можна представити у вигляді суми двох додатків: T(x, t) = стаціонарна температура (граничний розв’язок для великих часів) + перехідна температура (частина розв’язку, що залежить від початкових умов і прагне до нуля з ростом часу) = У даному випадку наша задача знайти перехідну температуру U(x, t) Підставляючи
у вихідну задачу (22)- (30), ми приходимо до нової задачі щодо невідомої функції U(x, t). Вирішивши цю задачу щодо нової невідомий функції U(x, t), можна додати її до стаціонарного розв’язку, у результаті чого вийде шукана функція T(x, t). Проробляючи ці прості перетворення з (27) – (30), одержимо
де Ця задача не тільки з однорідним рівнянням, але і з однорідними граничними умовами, що дозволяє вирішити її методом розділення перемінних, використовуючи розглянутий вище метод розділення перемінних, для функції U(x, t) одержуємо наступний вираз
де
Остаточно, розв’язок вихідної задачі виходить у такому вигляді
Що стосується граничних умов із залежними від часу правими частинами, то основні ідеї тут такі ж, як і в попередній задачі, але трохи більш складні. Перетворення залежних від часу граничних умов у нульові.
|


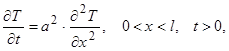
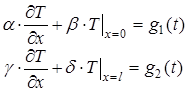 (неоднорідні граничні умови) (25)
(неоднорідні граничні умови) (25) (26)
(26) (27)
(27) , (28)
, (28) , (29)
, (29) (30)
(30)

 (31)
(31) (32)
(32) , (33)
, (33)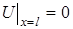 , (34)
, (34)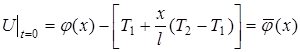 , (35)
, (35) нова, але відома початкова умова.
нова, але відома початкова умова.
 , (36)
, (36) (37)
(37) (38)
(38)


