Розв‘язок задач теплопровідності для необмежених середовищахМетоди інтегральних перетворень Фур'є є класичними аналітичними методами рішення задачі теплопровідності для різних середовищ (необмежених і напівобмежених). Основною перевагою цих методів є те, що вони дозволяють звести розв’язок складної вихідної задачі (рівняння теплопровідності в часткових похідних 2-го порядку), прямих аналітичних методів рішення якої в даний час немає, до простої задачі (звичайному диференціальному рівнянню 1-го порядку для зображення по Фур'є шуканої функції (температури), що вже легко вирішується стандартними методами. Потім, використовуючи зворотні перетворення Фур'є від отриманого зображення до шуканої функції, знаходять аналітичний вираз для розподілу температури в розглянутому середовищі. Загальна схема застосування методів інтегральних перетворень Фур'є представлена на рис.1. Задачі теплопереносу в необмежених середовищах необхідні для оцінки теплових полів у протяжних виробах при їх різних фізико-технічних методах обробки. До числа типових задач відносяться, наприклад, задача остигання виробу після його нерівномірної поверхневої обробки, тобто коли уздовж виробу в початковий момент часу має місце заданий розподіл температур, а також задача нагрівання виробу при впливі на нього деякого рухливого джерела тепла. При цьому, як правило, розглядаються випадки одномірних нестаціонарних теплових полів. Застосуємо метод інтегральних перетворень Фур'є для рішення вищезазначених задач. Задача 1. Процес остигання виробу після його нерівномірної поверхневої обробки описується наступним рівнянням теплопровідності (рис.2)
з початковою умовою
і граничними умовами Т®0,
Рисунок 1– Загальна схема застосування інтегральних перетворень Фур‘є
Рисунок 2 – Схема остигання виробу ( Потрібно, використовуючи метод інтегральних перетворень Фур'є, знайти загальне рішення задачі Т(х, t).
|
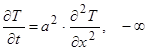< x < - ¥, t > 0 (1)
(2)
при х®±¥ (3)
- вузький тонкоплівочний елемент, тонкий, довгий стрижень та інше) з початковім розподіленням температури 
