Program DemoDrawPoly;
uses Graph, Crt; const N=7; { Количество вершин многоугольника +1} MultiRect: array[1..N] of PointType = {Координаты вершин} ((X: 200; Y: 100), {Координаты первой вершины и } (X: 285; Y: 155), (X: 285; Y: 255), (X: 200; Y: 300), (X: 115; Y: 255), (X: 115; Y: 155), (X: 200; Y: 100)); {последней (замыкающей) должны совпадать} var Gd, Gm, GrEr: Integer; begin Gd: = Detect; InitGraph(Gd, Gm, ’d: \bp\bgi’); GrEr: = GraphResult; if GrEr = grOk then begin DrawPoly(N, MultiRect); OutTextXY(50, 20, ’Нажмите любую клавишу...’); Repeat Until KeyPressed; CloseGraph; end else begin WriteLn(’Ошибка графики: ’, GrEr, ’. Нажмите Enter...’); Readln; end; end.
Сведения о других примитивах можно найти в книгах по Турбо Паскалю или в справочной системе Турбо Паскаля.
Все фигуры, как отмечалось выше, рисуются текущим цветом и типом линии. Цвет линии задается из имеющегося активного набора цветов – палитры.
Пример. Написать программу построения графика заданной функции Y=f(X) для аргумента X, изменяющегося от xn до xk. Для определенности будем считать, что Y=sin(x), xn = –2π, xk = 2π. Общие соображения по написанию программы для построения графиков приводились в п. 5.1.4. При построении графика должны быть определены масштабы – коэффициенты, с помощью которых натурные величины (X, Y) будут переводиться в графические координаты (xG, yG). В общем случае пределы изменения натурных величин: аргумента (xn, xk) и функции (Ymin, Ymax) должны быть отображены на выбранные пределы изменения графических координат: xGn – x графическое начальное, xGk – x графическое конечное, yGn – y графическое начальное, yGk – y графическое конечное. С учетом сказанного, масштабы можно определить по формулам: mx: =(xGk-xGn)/(xk-xn); { Масштаб по X } my: =(yGk-yGn)/(ymax-ymin); { Масштаб по Y } Максимальное и минимальное значения функции (хотя бы приблизительные, лучше с запасом в большую сторону) должны быть заданы пользователем. Для перехода к графическим координатам получим следующие соотношения: xG: =Round(xGn+(x-xn)*mx); yG: =Round(yGn+(ymax-y)*my); Для построения графика воспользуемся процедурой LineTo, которая будет проводить линию от точки к точке. Программа построения графика может быть такой.
Program PlotGrafik; uses Crt, Graph; Const xGn=20; { Константы, определяющие } yGn=50; { область экрана, } xGk=600; { в которую будет } yGk=470; { выводиться график } xn=-2*pi/2; { Начальное и } xk=2*pi/2; { конечное значение аргумента } ymin=-1; { Предполагаемые минимальное и } ymax=1; { максимальное значения функции } kT=150; { Количество точек графика } Var grDr, grMd, grEr: integer; x, y, Dx: real; xG, yG: integer; mx, my: real; { Масштабы по X и Y }
Function f(x: real): Real; begin f: =sin(x); {Функция, для которой строится график} end; Begin grDr: =Detect; InitGraph(GrDr, GrMd, ’D: \bp\BGI’); GrEr: =GraphResult; if GrEr=GrOk then { Графический режим удачно открыт} begin SetBkColor(Blue); ClearDevice; {Очистим экран, сделаем фон голубым} Dx: =(xk -xn)/(kT-1); { Шаг изменения аргумента } mx: =(xGk-xGn)/(xk-xn); { Масштаб по X } my: =(yGk-yGn)/(ymax-ymin); { Масштаб по Y } SetLineStyle(0, 0, 1); { Одинарная линия } SetColor(Red); { Оси нарисуем красным } Line(Round(xgn+(0-xn)*mx), ygn-20, Round(xgn+(0-xn)*mx), ygk); {Ось Y, на ней X=0} Line(xgn, Round(ygn+(ymax-0)*my), xgk+20, Round(ygn+(ymax-y)*my)); {Ось X, на ней Y=0} {Изображение стрелки на конце оси X и надписи X} MoveTo(xgk+20, Round(ygn+(ymax-y)*my)); LineRel(-8, 4); MoveTo(xgk+20, Round(ygn+(ymax-y)*my)); LineRel(-8, -4); MoveRel(0, -25); SetTextStyle(1, 0, 1); {Шрифт для обозначения осей} OutText(’X’); {Рисование стрелки на конце оси Y и надписи Y} MoveTo(Round(xgn+(0-xn)*mx), ygn-20); LineRel(-4, 8); MoveTo(Round(xgn+(0-xn)*mx), ygn-20); LineRel(4, 8); MoveRel(0, -15); OutText(’Y’); SetColor(white); { Белый цвет для линии графика } x: =xn; { Текущее значение для X } y: =F(x); { Значение функции для этого X } xG: =Round(xgn+(x-xn)*mx); {Графическая коорд. по X} yG: =Round(ygn+(ymax-y)*my); {Графическая коорд. по Y} MoveTo(xg, yg); { Курсор в эту точку экрана } While x< =xk do {Цикл для всех значений аргумента} begin x: =x+dx; y: =f(x); xG: =Round(xgn+(x-xn)*mx); yG: =Round(ygn+(ymax-y)*my); LineTo(xG, yG); end; SetTextStyle(0, 0, 1); { Шрифт для вывода текста } OutTextXY(5, 5, ’График функции Y=Sin(X)’); OutTextXY(5, 20, ’Нажмите любую клавишу...’); Repeat Until KeyPressed CloseGraph; { Закрываем графический режим } end else begin WriteLn(’Ошибка графики ’, GrEr, ’ ’, GraphErrorMsg(GrEr)); WriteLn(’Нажмите Enter...’); ReadLn; end; End.
Закраска замкнутой области выполняется процедурами: 5) SetFillStyle(Тип_закраски, Цвет: Word); – устанавливает тип (стиль) закраски и ее цвет.
В Турбо Паскале определено большое количество типов закраски, которые можно задавать либо с использованием предопределенных имен констант, либо их значений. Приведем некоторые из них: 0 – заполнение области фоновым цветом; 1 – сплошное заполнение области заданным цветом;
....... 11 – заполнение области частыми точками; 12 – заполнение области стилем, определяемым пользователем. Цвет - цвет закраски (из палитры).
Пример. SetFillStyle(4, 1);
6) FloodFill(x, y, Цвет_границы: Word); – закрашивает ограниченную область, используя текущий образец закраски. Точка (x, y) является внутренней точкой закрашиваемой области. Для заполнения области, ограниченной цветом, определяемым параметром Цвет_границы, используется текущий образец закраски. Например, программа, которая рисует концентрические окружности с координатами центра (150, 100) всеми 15-ю цветами (MaxColors) и закрашивает получившиеся кольца всеми 11-ю типами заливки и цветом, отличным от цвета контура будет иметь вид.
|

 2 – заполнение области горизонтальными линиями;
2 – заполнение области горизонтальными линиями;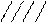 3 – заполнение области наклонными линиями;
3 – заполнение области наклонными линиями; 4 – заполнение области толстыми наклонными линиями
4 – заполнение области толстыми наклонными линиями


