Расчетные и графические задания. Типовые задачи и способы их решения
Типовые задачи и способы их решения Задание 1. Применяя правило максимизации полезности определить комбинацию товаров А и В, максимизирующую полезность при доходе равном 14 грн.
Таблица 13 – Полезность товаров А и В
Решение: Рассчитываем предельную полезность в расчете на 1 грн.товара А: для первой единицы его – 10, для второй – 8, для третьей- 7, для четвертой – 6, для пятой – 5, для шестой – 4, для седьмой – 3; товара В: для первой -12, для второй – 10, для третьей – 9, для четвертой – 8, для пятой – 6, для шестой – 3, для седьмой – 2. (Данные занести в таблицу). Покупку товаров осуществляем, применяя правило максимизации полезности. Комбинация товаров, максимизирующая полезность – 4А и 5В. Затем суммируем показатели предельной полезности 4А и 5В. От 4 единиц товара А получаем полезность в 31 ютиль (10 +8 +7 + 6), от 5 единиц товара В получаем 90 ютилей полезности (24 + 20 + 18 + 16 + 12). Доход в 14 грн. позволяет приобрести этот набор товаров. Деньги истрачены оптимальным образом, так как получено наибольшее удовлетворение – 121 ютиль. Полезность любого другого набора товаров меньше. Задание 2. У владельца фермерского хозяйства 2 лошади и 3 коровы. Цена лошади равна цене коровы. Найдите равновесный набор, если дана таблица Менгера.
Таблица 14 – Таблица Менгера
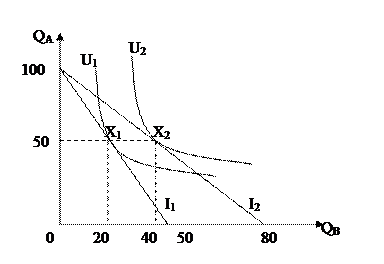
Решение: 1) Полезность имеющегося набора (2 лошади + 3 коровы) равна: U23 = (60+50) + (50+ 40+ 20) = 220. 2) Если фермер обменяет лошадь на корову, он получит полезность: U14 = 60 + (50+ 40 + 20 + 20)= 190. Полезность набора уменьшилась. 3) Если фермер обменяет корову на лошадь, он получит полезность: U32 = (60 +50 +30) + (50 + 40) = 230. Полезеность увеличится. 4) Если фермер еще раз обменяет корову на лошадь, он получит полезность: U41 = (60 + 50 + 30 + 10) + 50 = 200. Полезность уменьшается. Ответ: Следовательно, максимально возможная полезность равна 230. Равновесный набор состоит из 3 лошадей и 2 коров. Задание 3. Первое яблоко доставляет Маше удовлетворение, равное 8. Каждое следующее яблоко доставляет добавочное удовлетворение на 2 ед. меньше предыдущего. Начиная с какого яблока суммарное удовлетворение от потребления яблок будет уменьшаться? Решение: 1) Предельная полезность задается формулой убывающей арифметической прогрессии с первым членом 8 разностью 2. поэтому MU1 = 10 – 2q, где q – количество яблок; 2) Решаем неравенство 10 - 2q < 0, отсюда q > 5. Ответ: Начиная с 6 яблока полезность уменьшается. Задание 4. На основе приведенного графика ответьте на следующие вопросы: а) каков бюджет потребителя, если цена товара А равна 4 грн.; б) при каких условиях произойдет сдвиг бюджетной линии I1 в положение I2?
Рисунок 8 – Бюджетные линии и кривые безразличия
Решение: При нулевой покупке товара В, товара А приобретается 100 единиц. Отсюда бюджет потребителя составит I = (100 × 4) = 400 грн. При нулевой покупке товара А покупатель приобретает 50 единиц товара В по цене PB1 = 400 / 50 = 8 грн. Покупатель сможет приобрести 80единиц товара В при снижении цены до PB2 = 400 / 80 = 5 грн. Ответ: Бюджет потребителя равен 400 грн., сдвиг бюджетной линии из I1 в положение I2 произойдет при снижении цены на товар с 8 до 5 грн. Задание 5. Предположим, потребительский набор состоит из чая (х) и кофе (у), а функция полезности потребителя имеет вид U = 8х + 4у. При какой структуре набора потребитель окажется в состоянии равновесия, если выделяемые им на покупку данных благ расходы равны 160 грн. при цене чая - 20 грн, кофе – 40 грн. Решение: Потребитель окажется в состоянии потребительского равновесия, если структура набора будет удовлетворять равенству MUx/MUy = Px/Py. Для определения предельной нормы замещения благ (MRSxy = MUx/MUy) необходимо продифференцировать функцию полезности по х и у. Получаем: MUx = 8, MUy = 4. MRSxy = 8/4 = 2. Соотношение цен благ Рх / Ру = 20 / 40 = 0, 5. Так как функция полезности является линейной, то очевидно, что и наклон кривой безразличия, равный 2, больше наклона бюджетной линии (0, 5), можем сделать вывод о том, что потребитель будет находиться в состоянии углового оптимума. Так как значение MRSxy > Рх / Ру, набор потребителя будет состоять только из блага х. Его бюджетное уравнение примет вид 160 = х × Рх, то есть 160 = 20х. Отсюда х = 8. Ответ: Следовательно, структура оптимального набора: х = 8, у = 0. Задание 6. Функция полезности U = 5x + 4y + 6z, доход потребителя равен 60, цены продуктов x, y и z равны соответственно 3, 2 и 9. Найдите равновесный набор. Решение: Отношение предельной полезности к цене равно 5/3 для продукта х, 4/2 - для продукта у и 6/9 - для продукта z. Эти числа различны, касания (равновесия) нет. В этом случае равновесным будет набор на бюджетной плоскости, в котором имеется только продукт с наибольшим отношением предельной полезности к цене. Таким продуктом является у, так как 4/2 > 5/3 и 4/2 > 6/9. Равновесный набор состоит из 30 единиц товара z (60/2). Ответ: Набор 0, 30, 0 – равновесный. Задания для тренинга умений Задание 1. Потребитель расходует 20 грн. в неделю на покупку товаров А и Б. Получает ли он максимальное удовлетворение от покупки? Если нет, то как нужно изменить структуру покупок?
Таблица 15 – Цена и полезность товаров А и Б
Задание 2. Предположим, что предельная полезность видеокассеты равна 45 ютилям, а просмотра кинофильма – 30 ютилям. Видеокассета стоит 3 грн., а билет в кино – 1, 5 грн. Применяя правило максимизации полезности, в пользу чего вы сделаете выбор? Задание 3. Найдите на рисунках каждую из названных ниже кривых: а) функция полезности в случае одного продукта; б) функция предельной полезности; в) кривая безразличия; г) бюджетная линия; д) кривая безразличия в случае, когда блага образуют комплект; е) кривая безразличия, когда блага совершенно взаимозаменяемые.
Рисунок 9 – Различные кривые
Задание 4. Функция общей полезности товара для потребителя имеет вид TU = 100Q + 150Q2 – 2Q3. Составьте уравнение предельной полезности. Какова величина общей и предельной полезности при потреблении 5 единиц? Задание 5. Заполните таблицу, начертите графики.
Таблица 16 – Исходные данные
Задание 6. Находясь в равновесии, потребитель расходует 40 грн. на приобретение товара X (его цена составляет Рх = 20 грн.) и товара Y (его цена составляет Ру = 20 грн.). Построите кривую «цена – потребление» для этого потребителя и кривую спроса на товар X при условии, что цена на товар X последовательно снижается с 20 до 10 грн. и с 10 до 5 грн., а доход и цена товараY остается неизменными. Задание 7. Общая TU и предельная MU полезности товаров A, B, C представлены в таблице. Заполнить пропуски в таблице.
Таблица 17 – Исходные данные
Задание 8. У Петра 3 топора, у Романа 4 шапки. Найдите равновесные наборы, если даны таблицы Менгера.
Таблица 18 – Таблицы Менгера
Задание 9. Объясните при помощи графика, каким образом кривые безразличия могут быть использованы для построения кривой спроса. Задание 10. Допустим, потребитель имеет доход 200 грн. в месяц. На рисунке показаны две бюджетные линии и соответствующие им кривые безразличия.
Рисунок 10 – Кривые безразличия и бюджетные линии
Определить: а) какова цена товара Y? б) координаты двух точек линии спроса данного потребителя на товар X; в) зависит ли положение данной линии спроса от цены товара Y и от дохода потребителя? Задание 11. В таблице заданы равновесные объемы потребления продуктов Х и Y при некоторых ценах продукта Х. Цена продукта Y и доход неизменны. Необходимо: а) найти цену товара Y и доход потребителя; б) заполнить пустые клетки таблицы; в) построить кривую «цена-потребление»; г) построить бюджетную линию при цене 3; д) построить кривую спроса на товар Х; е) определить являются ли данные товары взаимодополняемыми?
Таблица 19 – Потребление продуктов Х и Y
Задание 12. В вашем ежедневном рационе питания всегда присутствует кофе и отсутствует чай (не пьете его никогда). Чему в данном случае будет равна предельная норма замещения кофе чаем, и как будет выглядеть кривая безразличия? Задание 13. Пусть домохозяйство приобретает три вида товаров X, Y, Z. Общая полезность U (в ютилях), которую получает домохозяйство от последовательного потребления этих товаров, указана в приведенной ниже таблице. Рассчитайте предельные полезности MUx, MUy, MUz, внесите значения в таблицу. Пусть Px = 2 тыс. грн., Py = 1 тыс. грн., Pz = 4 тыс. грн. Вычислите значения предельной полезности в расчете на 1 гривну для всех трех товаров и внесите полученные результаты в таблицу. Если бюджет домохозяйства составляет 17 тыс. грн., то какой набор товаров X, Y, Z обеспечит ему максимальную полезность?
Таблица 20 – Исходные данные
Задание 14. У студента Иванова в холодильнике сыр и колбаса нарезаны для удобства по 100 г. Общая полезность их потребления представлена в таблице 21. Определите количество съеденного им в день, если известно, что он в целом употребляет 700 г этих продуктов и при этом добивается максимума полезности.
Таблица 21 – Исходные данные
Задание 15. Функция полезности U = xy, доход потребителя равен 32, цены продуктов x и y равны 4 и 2 соответственно. Найдите равновесный набор. Задание 16. Функция полезности U = xyz, доход потребителя равен 48, цены продуктов x, y, z равны 4, 2 и 5 соответственно. Найдите равновесный набор. Задание 17. Желаемые наборы потребителя состоят из продуктов питания и развлечений. Его доход составляет 20 грн., цена продуктов питания 0, 5 грн., цена развлечений 0, 5 грн. Определить оптимальный выбор потребителя. Решить задачу аналитически и графически.
Таблица 22 - Предельная полезность товаров и услуг
Задание 18. В набор потребителя входят два товара: чай и конфеты. Общая полезность характеризуется данными, представленными в таблице 23. Цена одной кружки чая 2 грн., цена одной конфеты – 1, 5 грн. Общий доход потребителя, расходуемый на чай и конфеты составляет 7 грн. Какое количество кружек чая и конфет купит рациональный потребитель в состоянии равновесия?
Таблица 23 – Исходные данные
Задание 19. Доход потребителя равен 60. Яблоки стоят 3 грн., а груши 5 грн. Чему равна MRS (tga) при равновесии потребителя? Что произойдет, если цена груш снизится на 20%. Решить задачу аналитически и изобразить на графике. Задание 20. Доход потребителя составляет: I = 100 грн. В набор потребителя входит два товара Х и Y. При этом их равновесное количество соответственно составляет: Qx = 10 ед., Qy = 30 ед. Цена товара Х в 2 раза больше цены товара Y. Найдите цены этих товаров (Py –?, Px –?).
|