Пусть  – плоскость в пространстве
– плоскость в пространстве 
 – фиксированная (начальная) точка плоскости,
– фиксированная (начальная) точка плоскости, 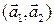 – базис множества
– базис множества  векторов плоскости. Очевидно, что точка
векторов плоскости. Очевидно, что точка  пространства принадлежит плоскости
пространства принадлежит плоскости  тогда и только тогда, когда вектор
тогда и только тогда, когда вектор 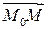 принадлежит множеству
принадлежит множеству  , т.е. представляется в виде
, т.е. представляется в виде
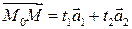 (1)
(1)
для некоторых  (рис.1). Зафиксируем в пространстве точку
(рис.1). Зафиксируем в пространстве точку 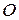 и обозначим
и обозначим 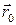 и
и 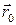 радиус-векторы соответственно точек
радиус-векторы соответственно точек  и
и 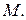 Тогда
Тогда  и равенство (1) можно переписать в виде
и равенство (1) можно переписать в виде
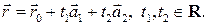 (2)
(2)
Формула (2) называется векторно-параметрическим уравнением плоскости  .
.
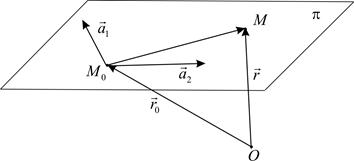
Рис. 1
Присоединим к точке  базис
базис  множества
множества  векторов пространства, получим аффинный репер
векторов пространства, получим аффинный репер  в пространстве
в пространстве  Пусть
Пусть 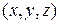 и
и 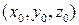 – координаты соответственно точек
– координаты соответственно точек  и
и  в данном репере. Согласно определения 2.1.2,
в данном репере. Согласно определения 2.1.2, 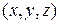 и
и 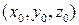 – координаты также радиус-векторов
– координаты также радиус-векторов 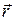 и
и 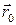 в базисе
в базисе  Пусть
Пусть 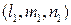 и
и  – координаты соответственно векторов
– координаты соответственно векторов  и
и 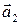 в базисе
в базисе  Тогда векторное равенство (2) равносильно трем скалярным равенствам:
Тогда векторное равенство (2) равносильно трем скалярным равенствам:
 (3)
(3)
Формулы (3) выражают координатно-параметрическое задание плоскости, они называются координатно - параметрическими уравнениями плоскости 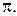 В этих формулах
В этих формулах 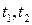 – параметры, которые могут принимать любые вещественные значения. При фиксировании значений параметров по формулам (3) вычисляются координаты конкретной точки плоскости.
– параметры, которые могут принимать любые вещественные значения. При фиксировании значений параметров по формулам (3) вычисляются координаты конкретной точки плоскости.
Еще один способ задания плоскости в пространстве получается, если заметить, что необходимым и достаточным условием принадлежности точки  плоскости
плоскости  является компланарность векторов
является компланарность векторов 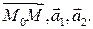 Последнее условие можно выразить через координаты векторов (утверждение 1.8.2) и тем самым записать уравнение плоскости:
Последнее условие можно выразить через координаты векторов (утверждение 1.8.2) и тем самым записать уравнение плоскости:
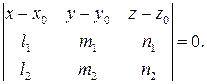 (4)
(4)
Раскрывая определитель, получим, что уравнение (4) есть линейное уравнение с тремя неизвестными вида
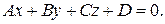 (5)
(5)
Уравнение (5) называется общим уравнением плоскости 
Хорошо известно, что любая плоскость однозначно определяется своими тремя точками, не лежащими на одной прямой. Пусть это будут точки 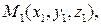
 и
и 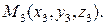 Выберем в качестве начальной точки плоскости
Выберем в качестве начальной точки плоскости 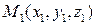 , а в качестве базисных векторов множества
, а в качестве базисных векторов множества  – векторы
– векторы 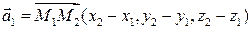 и
и  В этом случае можно записать общее уравнение плоскости по трем точкам:
В этом случае можно записать общее уравнение плоскости по трем точкам:
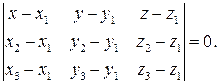 (4)
(4)
Для случая пространства справедлива теорема, аналогичная теореме 2.3.1 для плоскости.
Теорема 2.4.1. Пусть 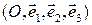 – аффинный репер в пространстве
– аффинный репер в пространстве 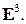
(i) Любая плоскость в пространстве 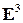 может быть задана в данном репере линейным уравнением вида
может быть задана в данном репере линейным уравнением вида
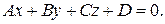 (5)
(5)
(ii) Обратно, любое линейное уравнение (5) при условии, что числа 
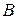 и С не равны нулю одновременно, задает в данном репере плоскость.
и С не равны нулю одновременно, задает в данном репере плоскость.
Доказательство. Истинность части (i) теоремы была отмечена выше.
(ii) Пусть, для определенности, 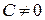 в уравнении (5). Тогда
в уравнении (5). Тогда
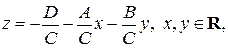
– общее решение уравнения (5). Поскольку 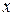 и
и  могут быть любыми числами, обозначим
могут быть любыми числами, обозначим  и будем рассматривать
и будем рассматривать 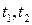 в качестве параметров. Все решения уравнения (5) теперь можно записать в виде:
в качестве параметров. Все решения уравнения (5) теперь можно записать в виде:

Сравнивая последние формулы с параметрическими уравнениями (3), можем сделать вывод, что уравнение (5) задает плоскость с начальной точкой  и базисными векторами
и базисными векторами 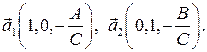 Если в уравнении (5)
Если в уравнении (5) 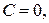 то
то 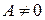 или
или 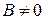 и доказательство проводится аналогично.
и доказательство проводится аналогично.
В следующем утверждении описывается геометрический смысл коэффициентов общего уравнения плоскости.
Утверждение 2.4.1. Пусть 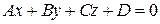 – общее уравнение плоскости
– общее уравнение плоскости  в репере
в репере 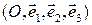 . Тогда:
. Тогда:
(i) 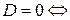 плоскость
плоскость  проходит через начало координат (
проходит через начало координат (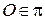 );
);
(ii) 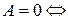 плоскость
плоскость  параллельна оси
параллельна оси  (если
(если  ), или содержит ось
), или содержит ось  (если
(если  );
);
(iii) 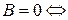 плоскость
плоскость  параллельна оси
параллельна оси  (если
(если  ), или содержит ось
), или содержит ось  (если
(если  );
);
(iv) 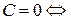 плоскость
плоскость  параллельна оси
параллельна оси 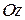 (если
(если  ), или содержит ось
), или содержит ось 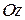 (если
(если  ).
).
Доказательство этого утверждения предлагается провести читателю самостоятельно в качестве упражнения.
Пусть в уравнении (5) все коэффициенты ненулевые, т.е. плоскость  не параллельна координатным осям и не проходит через начало координат. Тогда уравнение (5) можно переписать в виде:
не параллельна координатным осям и не проходит через начало координат. Тогда уравнение (5) можно переписать в виде:
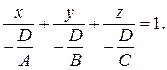
Если ввести обозначения 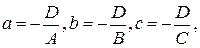 то получим уравнение плоскости
то получим уравнение плоскости  в следующем виде:
в следующем виде:
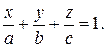 (6)
(6)
Уравнение (6) называется уравнением плоскости в отрезках, поскольку 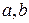 и
и 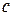 – величины отрезков, которые плоскость
– величины отрезков, которые плоскость  отсекает на координатных осях (рис. 2).
отсекает на координатных осях (рис. 2).
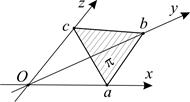
Рис. 2
Будем называть нормальным вектором плоскости любой вектор, перпендикулярный плоскости. Пусть (5) – общее уравнение плоскости  в ортонормированном репере
в ортонормированном репере 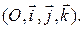 В этом случае вектор
В этом случае вектор 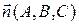 – нормальный вектор плоскости
– нормальный вектор плоскости 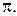 Чтобы убедиться в этом, достаточно проверить, что этот вектор ортогонален вектору
Чтобы убедиться в этом, достаточно проверить, что этот вектор ортогонален вектору 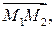 построенному по любым точкам
построенному по любым точкам 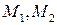 плоскости
плоскости 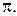 Пусть точки
Пусть точки 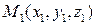 и
и  заданы своими координатами в репере
заданы своими координатами в репере 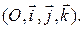 Тогда
Тогда 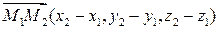 и
и

т.е. 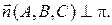
Если для плоскости  заданы начальная точка
заданы начальная точка 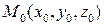 своими координатами в ортонормированном репере
своими координатами в ортонормированном репере 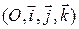 и нормальный вектор плоскости
и нормальный вектор плоскости 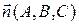 своими координатами в базисе
своими координатами в базисе 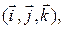 то можно записать уравнение плоскости
то можно записать уравнение плоскости  в данном репере в виде:
в данном репере в виде:
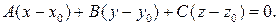 (7)
(7)
В самом деле, очевидно, что точка 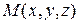 лежит в плоскости
лежит в плоскости  тогда и только тогда, когда векторы
тогда и только тогда, когда векторы 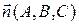 и
и 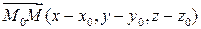 перпендикулярны (рис. 3). Равенство (7) как раз и выражает это условие.
перпендикулярны (рис. 3). Равенство (7) как раз и выражает это условие.
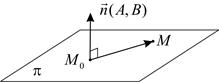
Рис. 3

 – плоскость в пространстве
– плоскость в пространстве 
 – фиксированная (начальная) точка плоскости,
– фиксированная (начальная) точка плоскости, 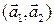 – базис множества
– базис множества  векторов плоскости. Очевидно, что точка
векторов плоскости. Очевидно, что точка  пространства принадлежит плоскости
пространства принадлежит плоскости 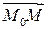 принадлежит множеству
принадлежит множеству 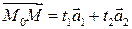 (1)
(1) (рис.1). Зафиксируем в пространстве точку
(рис.1). Зафиксируем в пространстве точку 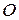 и обозначим
и обозначим 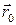 и
и 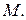 Тогда
Тогда  и равенство (1) можно переписать в виде
и равенство (1) можно переписать в виде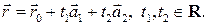 (2)
(2)
 множества
множества 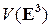 векторов пространства, получим аффинный репер
векторов пространства, получим аффинный репер 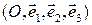 в пространстве
в пространстве  Пусть
Пусть 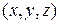 и
и 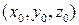 – координаты соответственно точек
– координаты соответственно точек 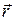 и
и  Пусть
Пусть 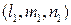 и
и  – координаты соответственно векторов
– координаты соответственно векторов  и
и 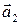 в базисе
в базисе  (3)
(3)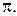 В этих формулах
В этих формулах 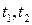 – параметры, которые могут принимать любые вещественные значения. При фиксировании значений параметров по формулам (3) вычисляются координаты конкретной точки плоскости.
– параметры, которые могут принимать любые вещественные значения. При фиксировании значений параметров по формулам (3) вычисляются координаты конкретной точки плоскости.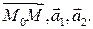 Последнее условие можно выразить через координаты векторов (утверждение 1.8.2) и тем самым записать уравнение плоскости:
Последнее условие можно выразить через координаты векторов (утверждение 1.8.2) и тем самым записать уравнение плоскости: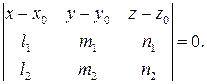 (4)
(4)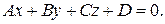 (5)
(5)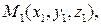
 и
и 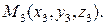 Выберем в качестве начальной точки плоскости
Выберем в качестве начальной точки плоскости 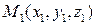 , а в качестве базисных векторов множества
, а в качестве базисных векторов множества 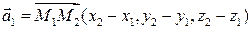 и
и  В этом случае можно записать общее уравнение плоскости по трем точкам:
В этом случае можно записать общее уравнение плоскости по трем точкам: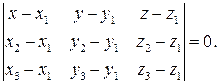 (4)
(4)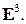
 может быть задана в данном репере линейным уравнением вида
может быть задана в данном репере линейным уравнением вида
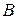 и С не равны нулю одновременно, задает в данном репере плоскость.
и С не равны нулю одновременно, задает в данном репере плоскость.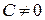 в уравнении (5). Тогда
в уравнении (5). Тогда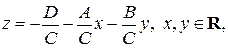
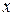 и
и  могут быть любыми числами, обозначим
могут быть любыми числами, обозначим  и будем рассматривать
и будем рассматривать 
 и базисными векторами
и базисными векторами 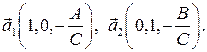 Если в уравнении (5)
Если в уравнении (5) 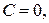 то
то 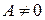 или
или 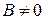 и доказательство проводится аналогично.
и доказательство проводится аналогично. 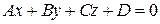 – общее уравнение плоскости
– общее уравнение плоскости 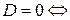 плоскость
плоскость 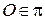 );
);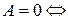 плоскость
плоскость  (если
(если  ), или содержит ось
), или содержит ось  );
);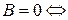 плоскость
плоскость  (если
(если 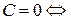 плоскость
плоскость 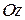 (если
(если 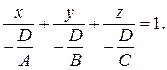
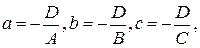 то получим уравнение плоскости
то получим уравнение плоскости 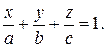 (6)
(6)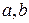 и
и 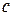 – величины отрезков, которые плоскость
– величины отрезков, которые плоскость 
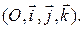 В этом случае вектор
В этом случае вектор 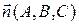 – нормальный вектор плоскости
– нормальный вектор плоскости 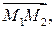 построенному по любым точкам
построенному по любым точкам 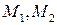 плоскости
плоскости 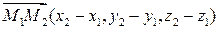 и
и
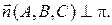
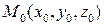 своими координатами в ортонормированном репере
своими координатами в ортонормированном репере  и нормальный вектор плоскости
и нормальный вектор плоскости 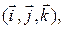 то можно записать уравнение плоскости
то можно записать уравнение плоскости 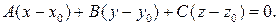 (7)
(7) лежит в плоскости
лежит в плоскости 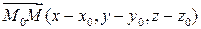 перпендикулярны (рис. 3). Равенство (7) как раз и выражает это условие.
перпендикулярны (рис. 3). Равенство (7) как раз и выражает это условие.



