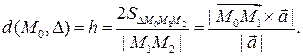Как и на плоскости, прямая в пространстве может быть задана параметрически, а также общими уравнениями. Вывод векторно-параметрического уравнения прямой в пространстве совершенно аналогичен случаю прямой на плоскости.
Пусть  – прямая в пространстве
– прямая в пространстве  ,
,  – фиксированная точка,
– фиксированная точка,  – направляющий вектор прямой
– направляющий вектор прямой 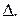 Необходимое и достаточное условие того, что точка пространства
Необходимое и достаточное условие того, что точка пространства  лежит на прямой
лежит на прямой  формулируется следующим образом:
формулируется следующим образом:

 (векторы
(векторы 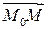 и
и  коллинеарны) (рис. 4).
коллинеарны) (рис. 4).


Рис. 4 Рис. 5
Пусть 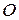 – фиксированная точка пространства,
– фиксированная точка пространства,  – радиус-вектор начальной точки
– радиус-вектор начальной точки 
 – радиус-вектор произвольной точки
– радиус-вектор произвольной точки  пространства. Коллинеарность векторов
пространства. Коллинеарность векторов 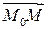 и
и  означает, что
означает, что  для некоторого
для некоторого  Учитывая, что
Учитывая, что  имеем следующую цепочку эквивалентностей:
имеем следующую цепочку эквивалентностей:
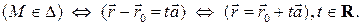
Таким образом, мы получили векторно-параметрическое задание прямой:
 (15)
(15)
Равенство (15) называют также векторно-параметрическим уравнением прямой 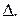 Формула (1) по виду совпадает с соответствующей формулой для прямой на плоскости, отличие только в том, что векторы, участвующие в этой формуле, являются векторами пространства, а не плоскости. Присоединим к точке
Формула (1) по виду совпадает с соответствующей формулой для прямой на плоскости, отличие только в том, что векторы, участвующие в этой формуле, являются векторами пространства, а не плоскости. Присоединим к точке 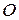 базис
базис  множества векторов пространства
множества векторов пространства  получим аффинный репер
получим аффинный репер 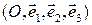 в пространстве
в пространстве  Пусть
Пусть 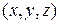 и
и 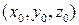 – координаты соответственно точек
– координаты соответственно точек  и
и  в данном репере,
в данном репере,  – координаты направляющего вектора прямой
– координаты направляющего вектора прямой  в базисе
в базисе  Тогда векторное равенство (1) равносильно трем скалярным равенствам:
Тогда векторное равенство (1) равносильно трем скалярным равенствам:
 (16)
(16)
Формулы (2) выражают координатно-параметрическое задание прямой, они называются также координатно - параметрическими уравнениями прямой 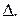
Исключая из уравнений (16) параметр  получаем равенства
получаем равенства
 (17)
(17)
которые называются каноническим уравнением прямой в пространстве. Равенства (17), эквивалентны системе уравнений
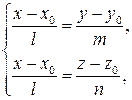
Каждое из уравнений системы (как и в случае прямой на плоскости, равенства дробей рассматриваются как пропорции) является линейным уравнением, задающим плоскость. Таким образом, прямая  задается здесь как пересечение плоскостей. В общем случае, согласно теореме 2.4.2, система линейных уравнений, задающая прямую, имеет вид
задается здесь как пересечение плоскостей. В общем случае, согласно теореме 2.4.2, система линейных уравнений, задающая прямую, имеет вид
 (18)
(18)
причем коэффициенты при неизвестных в уравнениях системы не пропорциональны. Уравнения (18) называются общими уравнениями прямой.
Пусть  и
и  – прямые в пространстве, заданные начальными точками и направляющими векторами соответственно
– прямые в пространстве, заданные начальными точками и направляющими векторами соответственно 
 и
и  Есть четыре варианта их взаимного расположения в пространстве: они могут совпадать, быть параллельными, пересекаться в одной точке либо скрещиваться. По координатам их направляющих векторов (соответственно,
Есть четыре варианта их взаимного расположения в пространстве: они могут совпадать, быть параллельными, пересекаться в одной точке либо скрещиваться. По координатам их направляющих векторов (соответственно,  и
и  ) легко отличить первые две возможности от двух других: прямые
) легко отличить первые две возможности от двух других: прямые  и
и  совпадают или параллельны тогда и только тогда, когда координаты их направляющих векторов пропорциональны:
совпадают или параллельны тогда и только тогда, когда координаты их направляющих векторов пропорциональны:
 для некоторого
для некоторого 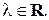
Приведем также критерий того, что две прямые скрещиваются.
Утверждение 2.4.2. Пусть  и
и  – прямые в пространстве, заданные начальными точками и направляющими векторами соответственно
– прямые в пространстве, заданные начальными точками и направляющими векторами соответственно 
 и
и  Прямые
Прямые  и
и  скрещиваются тогда и только тогда, когда векторы
скрещиваются тогда и только тогда, когда векторы  и
и  не компланарны.
не компланарны.
Доказательство. Условие компланарности векторов  и
и  , очевидно, эквивалентно тому, что прямые
, очевидно, эквивалентно тому, что прямые  и
и  лежат в одной плоскости. Следовательно, векторы
лежат в одной плоскости. Следовательно, векторы  и
и  не компланарны тогда и только тогда, когда прямые
не компланарны тогда и только тогда, когда прямые  и
и  не лежат в одной плоскости, т.е. скрещиваются.
не лежат в одной плоскости, т.е. скрещиваются.
Получим формулу для вычисления расстояния от точки  до прямой
до прямой  заданной начальной точкой
заданной начальной точкой  и направляющим вектором
и направляющим вектором 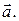 Пусть
Пусть  не лежит на прямой
не лежит на прямой 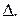 Отложим вектор
Отложим вектор  от точки
от точки  , получим точку прямой
, получим точку прямой  причем точки
причем точки  образуют треугольник. Расстояние от точки
образуют треугольник. Расстояние от точки  до прямой
до прямой  – это длина высоты
– это длина высоты  треугольника
треугольника  проведенной из точки
проведенной из точки  (рис. 5).Следовательно,
(рис. 5).Следовательно,
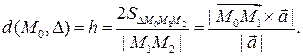

 – прямая в пространстве
– прямая в пространстве  ,
,  – фиксированная точка,
– фиксированная точка,  – направляющий вектор прямой
– направляющий вектор прямой 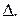 Необходимое и достаточное условие того, что точка пространства
Необходимое и достаточное условие того, что точка пространства  лежит на прямой
лежит на прямой 
 (векторы
(векторы 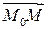 и
и 

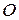 – фиксированная точка пространства,
– фиксированная точка пространства,  – радиус-вектор начальной точки
– радиус-вектор начальной точки 
 – радиус-вектор произвольной точки
– радиус-вектор произвольной точки  для некоторого
для некоторого  Учитывая, что
Учитывая, что  имеем следующую цепочку эквивалентностей:
имеем следующую цепочку эквивалентностей: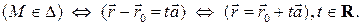
 (15)
(15) множества векторов пространства
множества векторов пространства  получим аффинный репер
получим аффинный репер 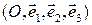 в пространстве
в пространстве  Пусть
Пусть 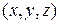 и
и 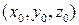 – координаты соответственно точек
– координаты соответственно точек  – координаты направляющего вектора прямой
– координаты направляющего вектора прямой  Тогда векторное равенство (1) равносильно трем скалярным равенствам:
Тогда векторное равенство (1) равносильно трем скалярным равенствам: (16)
(16) получаем равенства
получаем равенства (17)
(17)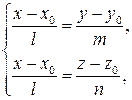
 (18)
(18) и
и  – прямые в пространстве, заданные начальными точками и направляющими векторами соответственно
– прямые в пространстве, заданные начальными точками и направляющими векторами соответственно  и
и  Есть четыре варианта их взаимного расположения в пространстве: они могут совпадать, быть параллельными, пересекаться в одной точке либо скрещиваться. По координатам их направляющих векторов (соответственно,
Есть четыре варианта их взаимного расположения в пространстве: они могут совпадать, быть параллельными, пересекаться в одной точке либо скрещиваться. По координатам их направляющих векторов (соответственно,  и
и  ) легко отличить первые две возможности от двух других: прямые
) легко отличить первые две возможности от двух других: прямые  для некоторого
для некоторого 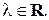
 и
и  не компланарны.
не компланарны. заданной начальной точкой
заданной начальной точкой  и направляющим вектором
и направляющим вектором 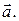 Пусть
Пусть  причем точки
причем точки  образуют треугольник. Расстояние от точки
образуют треугольник. Расстояние от точки  треугольника
треугольника  проведенной из точки
проведенной из точки