Следующая теорема показывает, как по общим уравнениям плоскостей можно определить тип их взаимного расположения.
Теорема 2.4.2. Пусть плоскости  и
и  заданы в некотором аффинном репере общими уравнениями:
заданы в некотором аффинном репере общими уравнениями:
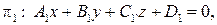 (8)
(8)
 (9)
(9)
Тогда верны следующие эквивалентности:
(i) плоскости  и
и  совпадают тогда и только тогда, когда существует ненулевое число
совпадают тогда и только тогда, когда существует ненулевое число 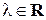 такое, что
такое, что 
 (соответствующие коэффициенты уравнений прямых пропорциональны);
(соответствующие коэффициенты уравнений прямых пропорциональны);
(ii) плоскости  и
и  параллельны тогда и только тогда, когда существует ненулевое число
параллельны тогда и только тогда, когда существует ненулевое число 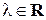 такое, что
такое, что 
 но
но  (соответствующие коэффициенты уравнений при неизвестных пропорциональны, однако их отношение не равно отношению свободных членов);
(соответствующие коэффициенты уравнений при неизвестных пропорциональны, однако их отношение не равно отношению свободных членов);
(iii) плоскости  и
и  пересекаются по прямой тогда и только тогда, когда не существует числа
пересекаются по прямой тогда и только тогда, когда не существует числа 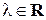 такого, что
такого, что 
 (коэффициенты при неизвестных не пропорциональны).
(коэффициенты при неизвестных не пропорциональны).
Доказательство. Заметим, что как и в случае теоремы 2.3.2, достаточно доказать справедливость любых двух из трех пунктов теоремы 2.4.2. Тогда третий пункт будет справедлив, поскольку это единственная возможная альтернатива двум другим.
Докажем вначале теорему в случае, когда уравнения плоскостей даны в ортонормированном репере 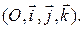 Как отмечено выше, в рассматриваемом случае векторы
Как отмечено выше, в рассматриваемом случае векторы  и
и  – нормальные векторы соответственно для плоскостей
– нормальные векторы соответственно для плоскостей  и
и  Очевидно, что плоскости совпадают или параллельны тогда и только тогда, когда их направляющие векторы коллинеарны, т.е.
Очевидно, что плоскости совпадают или параллельны тогда и только тогда, когда их направляющие векторы коллинеарны, т.е.  для некоторого ненулевого числа
для некоторого ненулевого числа 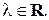 Это означает, что выполняются равенства:
Это означает, что выполняются равенства:
 (10)
(10)
т.е. коэффициенты при неизвестных пропорциональны. При условии (10) рассмотрим систему уравнений
 (11)
(11)
Эта система задает пересечение плоскостей 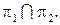 Очевидно, что плоскости параллельны тогда и только тогда, когда система (11) не имеет решений; плоскости совпадают тогда и только тогда, когда система (11) имеет бесконечно много решений. Подставляя во второе уравнение
Очевидно, что плоскости параллельны тогда и только тогда, когда система (11) не имеет решений; плоскости совпадают тогда и только тогда, когда система (11) имеет бесконечно много решений. Подставляя во второе уравнение  и вычитая из него первое уравнение, умноженное на
и вычитая из него первое уравнение, умноженное на  получим, что следствием системы (11) является условие
получим, что следствием системы (11) является условие  Это условие приводит к противоречию (система (11) не имеет решений), если
Это условие приводит к противоречию (система (11) не имеет решений), если  Следовательно, если плоскости совпадают, то необходимо выполнение условий:
Следовательно, если плоскости совпадают, то необходимо выполнение условий: 

 Обратно, если соответствующие коэффициенты уравнений пропорциональны, то множества решений этих уравнений совпадают, т.е.
Обратно, если соответствующие коэффициенты уравнений пропорциональны, то множества решений этих уравнений совпадают, т.е.  Таким образом, доказана справедливость пунктов (i) и (ii), а, следовательно и всей теоремы 2.4.2 в случае ортонормированного репера.
Таким образом, доказана справедливость пунктов (i) и (ii), а, следовательно и всей теоремы 2.4.2 в случае ортонормированного репера.
Для завершения доказательства нам потребуется связь между уравнениями одной и той же плоскости в двух различных реперах. Пусть 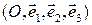 и
и 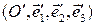 – два репера и пусть плоскость
– два репера и пусть плоскость  в репере
в репере 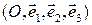 задана уравнением
задана уравнением 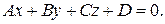 Воспользуемся формулами преобразования координат точек (формулы (2) или
Воспользуемся формулами преобразования координат точек (формулы (2) или  из § 2.1) при переходе от первого репера ко второму:
из § 2.1) при переходе от первого репера ко второму:
 (12)
(12)
Подставив выражения  из этих формул в исходное уравнение, получим уравнение плоскости
из этих формул в исходное уравнение, получим уравнение плоскости  в репере
в репере 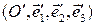 :
:

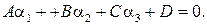
Таким образом, уравнение плоскости  в репере
в репере 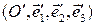 имеет вид
имеет вид  где
где 
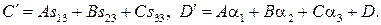
Теперь можно завершить доказательство теоремы. Пусть плоскости  и
и  заданы своими уравнениями (8) и (9) в произвольном аффинном репере
заданы своими уравнениями (8) и (9) в произвольном аффинном репере  Рассмотрим наряду с этим репером ортонормированный репер
Рассмотрим наряду с этим репером ортонормированный репер 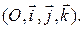 В таком случае формулы преобразования координат точек при переходе от репера
В таком случае формулы преобразования координат точек при переходе от репера 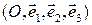 к реперу
к реперу 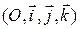 имеют вид (12), причем:
имеют вид (12), причем: 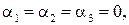 так как точки О и
так как точки О и  совпадают. Следовательно, уравнения плоскостей
совпадают. Следовательно, уравнения плоскостей  и
и  в репере
в репере 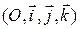 имеют вид:
имеют вид:
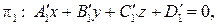
 где
где
 (13)
(13)
Используя формулы преобразования координат при обратном переходе от репера 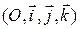 к реперу
к реперу  получим формулы вида (13), выражающие нештрихованные коэффициенты уравнений плоскостей через штрихованные:
получим формулы вида (13), выражающие нештрихованные коэффициенты уравнений плоскостей через штрихованные:
 (14)
(14)
Здесь  – элементы обратной матрицы для матрицы
– элементы обратной матрицы для матрицы  Формулы (13) и (14) показывают, все коэффициенты (или только коэффициенты при неизвестных) в уравнениях плоскостей в репере
Формулы (13) и (14) показывают, все коэффициенты (или только коэффициенты при неизвестных) в уравнениях плоскостей в репере 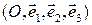 пропорциональны тогда и только тогда, когда они пропорциональны в уравнениях плоскостей в репере
пропорциональны тогда и только тогда, когда они пропорциональны в уравнениях плоскостей в репере 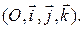 Это означает, что теорема справедлива в случае произвольного репера, поскольку для случая ортонормированного репера она доказана.
Это означает, что теорема справедлива в случае произвольного репера, поскольку для случая ортонормированного репера она доказана.

 и
и  заданы в некотором аффинном репере общими уравнениями:
заданы в некотором аффинном репере общими уравнениями: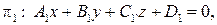 (8)
(8) (9)
(9)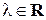 такое, что
такое, что 
 (соответствующие коэффициенты уравнений прямых пропорциональны);
(соответствующие коэффициенты уравнений прямых пропорциональны);
 но
но  (соответствующие коэффициенты уравнений при неизвестных пропорциональны, однако их отношение не равно отношению свободных членов);
(соответствующие коэффициенты уравнений при неизвестных пропорциональны, однако их отношение не равно отношению свободных членов);
 (коэффициенты при неизвестных не пропорциональны).
(коэффициенты при неизвестных не пропорциональны). Как отмечено выше, в рассматриваемом случае векторы
Как отмечено выше, в рассматриваемом случае векторы  и
и  – нормальные векторы соответственно для плоскостей
– нормальные векторы соответственно для плоскостей  Очевидно, что плоскости совпадают или параллельны тогда и только тогда, когда их направляющие векторы коллинеарны, т.е.
Очевидно, что плоскости совпадают или параллельны тогда и только тогда, когда их направляющие векторы коллинеарны, т.е.  для некоторого ненулевого числа
для некоторого ненулевого числа  Это означает, что выполняются равенства:
Это означает, что выполняются равенства: (10)
(10) (11)
(11)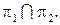 Очевидно, что плоскости параллельны тогда и только тогда, когда система (11) не имеет решений; плоскости совпадают тогда и только тогда, когда система (11) имеет бесконечно много решений. Подставляя во второе уравнение
Очевидно, что плоскости параллельны тогда и только тогда, когда система (11) не имеет решений; плоскости совпадают тогда и только тогда, когда система (11) имеет бесконечно много решений. Подставляя во второе уравнение  и вычитая из него первое уравнение, умноженное на
и вычитая из него первое уравнение, умноженное на  получим, что следствием системы (11) является условие
получим, что следствием системы (11) является условие  Это условие приводит к противоречию (система (11) не имеет решений), если
Это условие приводит к противоречию (система (11) не имеет решений), если  Следовательно, если плоскости совпадают, то необходимо выполнение условий:
Следовательно, если плоскости совпадают, то необходимо выполнение условий: 
 Обратно, если соответствующие коэффициенты уравнений пропорциональны, то множества решений этих уравнений совпадают, т.е.
Обратно, если соответствующие коэффициенты уравнений пропорциональны, то множества решений этих уравнений совпадают, т.е.  Таким образом, доказана справедливость пунктов (i) и (ii), а, следовательно и всей теоремы 2.4.2 в случае ортонормированного репера.
Таким образом, доказана справедливость пунктов (i) и (ii), а, следовательно и всей теоремы 2.4.2 в случае ортонормированного репера.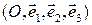 и
и 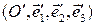 – два репера и пусть плоскость
– два репера и пусть плоскость  в репере
в репере 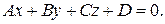 Воспользуемся формулами преобразования координат точек (формулы (2) или
Воспользуемся формулами преобразования координат точек (формулы (2) или  из § 2.1) при переходе от первого репера ко второму:
из § 2.1) при переходе от первого репера ко второму: (12)
(12) из этих формул в исходное уравнение, получим уравнение плоскости
из этих формул в исходное уравнение, получим уравнение плоскости 
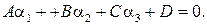
 где
где 
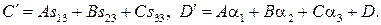
 Рассмотрим наряду с этим репером ортонормированный репер
Рассмотрим наряду с этим репером ортонормированный репер 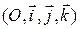 имеют вид (12), причем:
имеют вид (12), причем: 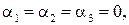 так как точки О и
так как точки О и  совпадают. Следовательно, уравнения плоскостей
совпадают. Следовательно, уравнения плоскостей 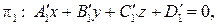
 где
где (13)
(13) получим формулы вида (13), выражающие нештрихованные коэффициенты уравнений плоскостей через штрихованные:
получим формулы вида (13), выражающие нештрихованные коэффициенты уравнений плоскостей через штрихованные: (14)
(14) – элементы обратной матрицы для матрицы
– элементы обратной матрицы для матрицы  Формулы (13) и (14) показывают, все коэффициенты (или только коэффициенты при неизвестных) в уравнениях плоскостей в репере
Формулы (13) и (14) показывают, все коэффициенты (или только коэффициенты при неизвестных) в уравнениях плоскостей в репере 


