Интегрированные пакеты математических расчетов

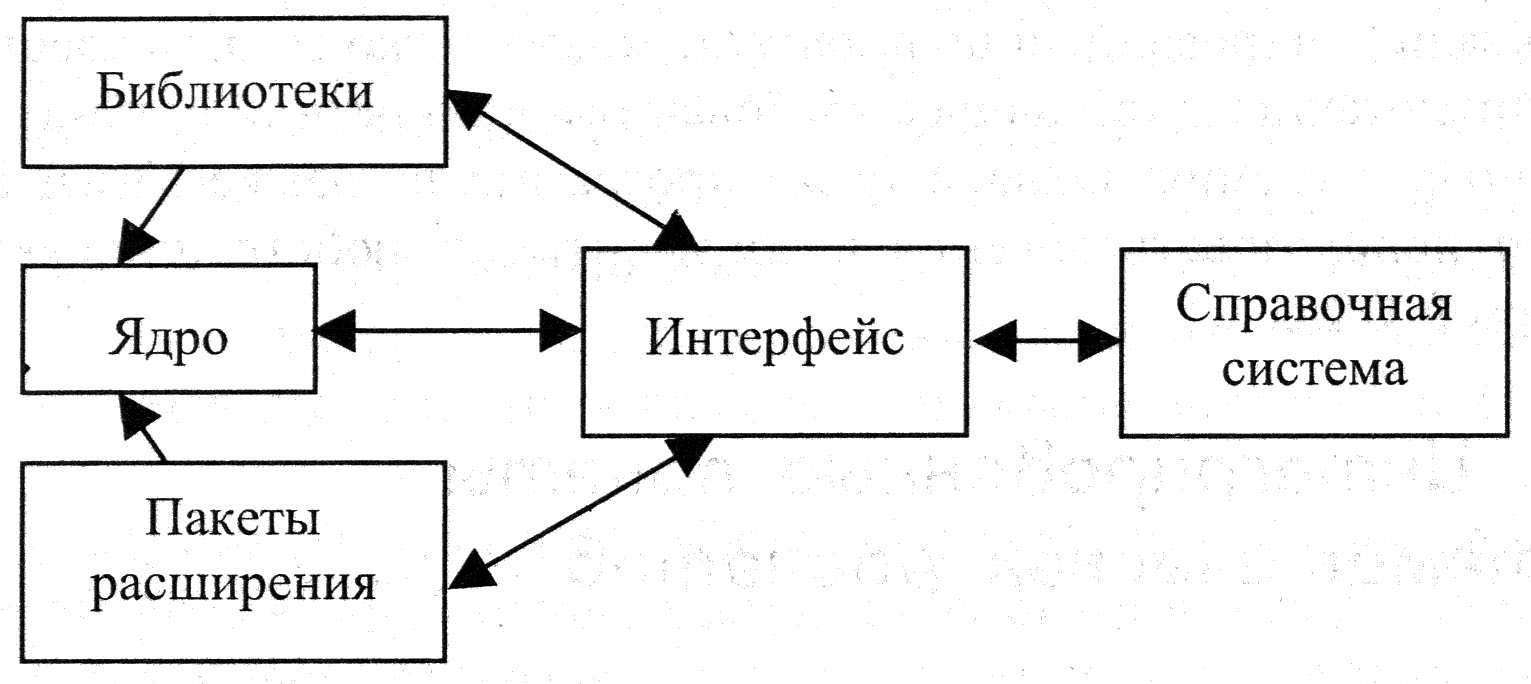
Практическим результатом компьютерной математики явилась разработка большого количества компьютерных математических систем.

Структура систем компьютерной математики выглядит следующим образом:

Ядро представляет совокупность процедур, обеспечивающих на­бор встроенных операторов системы. Интерфейс дает возможность пользователю обра­щаться к ядру с запросами и выдает решения на экране монитора. Программы, работающие в ядре, выполняются быстро, вызываются очень часто, и потому их ограниченное количество. Большое коли­чество программ, используемых относительно редко, собраны в биб­лиотеки. Расширение возможностей системы достигается за счет па­кетов расширения. Эти пакеты пишутся на собственном языке расширения и могут создаваться самими пользователями. Справочная система обеспечивает получение оперативной информации по сис­теме.

По уровню сложности выделяют три класса математических систем:

- начального уровня для школьников и студентов (Derive, MuPad);

- среднего уровня (MuPad, MathCad);

- высший класс (Mathematica, Maple, MatLab).

В настоящее время ком­пьютерные математические системы по функциональному назначе­нию можно подразделить на семь классов:

1. Табличные процессоры.

2. Системы для численных расчетов способны выполнять арифметические, алгебраические, логические операторы и функции, векторные и матричные операторы и функ­ции, средства решения уравнений, систем линейных и нелинейных уравнений, средства решения систем дифференциальных уравнений, средства оптимизации и линейного программирования, средства со­здания графиков и средства программирования (Eureka, Mercury, MathCad).

3. Матричные системы – все функции системы определяются как матричные, т.е. способные выполнять действия над масси­вами (MatLab).

4. Системы для статистических расчетов – предназначены для статистической обработки данных (StatGraphics Plus, Statistica, SPSS).

5. Системы для специальных расчетов – часть математических паке­тов ориентированная на некоторый узкоспециальный круг задач (система нелинейных уравнений ТК Solver, система дифферен­циальных уравнений Dynamic Solver, построение графиков Axum и т.д.).

6. Системы для аналитических расчетов (компьютерной алгебры) – дают возможность произво­дить вычисления в аналитическом виде (Maple, MathCad).

7. Универсальные системы.