Волновое уравнение. Уравнение Шредингера
Уравнение, которое будет описывать движение электрона, должно удовлетворять следующим требованиям: отражать волновой характер движения электрона и содержать в себе характеристики электрона как частицы. Для описания волновых свойств электрона можно использовать известное из математики и физики дифференциальное уравнение второго порядка (уравнение волнового процесса):
v – скорость распространения волны. Y(x, y, z, t) – пси-функция – волновая функция, которая зависит от координат и времени и может быть представлена в виде синуса, косинуса, экспоненты или любой другой функции, являющейся решением дифференциального уравнения волнового процесса. Для простоты написания левую часть уравнения представляют обычно в операторной форме: Ñ 2Y = где Чаще всего интерес представляют стационарные процессы (стоячие волны). Описывающее их уравнение содержит функцию, не зависящую от времени. Поэтому волновое уравнение преобразуют, исключая зависимость от времени. Делается допущение, что волновую функцию можно представить в виде произведения двух функций, одна из которых зависит только от координат (Y(x, y, z)), а другая только от времени (G (t)): Y(x, y, z, t) = Y(x, y, z)× G (t). Волновое уравнение приобретает вид
G (t)не зависит от координат, поэтому выносится за знак дифференцирования в левой части уравнения, а Y(x, y, z) не зависит от времени – выносится за знак дифференцирования в правой части. Из теории волновых процессов известно, что функцию G (t) можно представить в виде G (t) = А × cos(2p× n× t), где n - частота волнового процесса. Дважды дифференцируя G (t) по времени: G (t) = А × cos(2p× n× t) ¹ 0,
и подставляя вторую производную G (t) в уравнение волнового процесса, получаем А × cos(2p× n× t)× Ñ 2Y(x, y, z) = (1/v2) × Y(x, y, z)× (- A × 4p2n2) × cos(2p× n× t), Ñ 2Y(x, y, z) = -(4p2n2/ v 2) × Y(x, y, z), Ñ 2Y(x, y, z) + (4p2n2/ v 2) × Y(x, y, z) = 0. Поскольку частота волнового процесса равна скорости распространения волны, деленной на длину волны: Ñ 2Y(x, y, z) + (4p2/l2) × Y(x, y, z) = 0 В полученном уравнении длину волны частицы можно заменить такими ее характеристиками, как масса и кинетическая энергия, используя уравнение де Бройля. Длина волны де Бройля Кинетическая энергия электрона
Как правило, при описании состояния электрона определяют полную энергию. Поскольку кинетическая энергия электрона равна разности между полной энергией (E) и его потенциальной энергией (V): E к = E – V, то можно записать
Таким образом, получается волновое уравнение, независимое от времени, содержащее в качестве параметра массу электрона, характеристику электрона как частицы. Это уравнение известно как уравнение Шрёдингера, названное по имени австрийского физика Эрвина Шрёдингера (Schrö dinger), который его предложил в 1926 г. для описания состояния микрочастицы в потенциальном поле. Прежде чем решать уравнение Шредингера для конкретных систем, выясним физический смысл волновой функции. Раскрыть его достаточно непросто, поскольку в макромире нет аналогий корпускулярно-волновым свойствам микрообъектов. И до некоторой степени волновая функция представляет собой математическую абстракцию. В 1926 г. Макс Борн (Born), применив вероятностные идеи принципа неопределенности, дал общепринятую в настоящее время трактовку физического смысла волновой функции. Во-первых, сама волновая функция физического смысла не имеет, но связана с вероятностью нахождения частицы в данном элементе пространства. Во-вторых, вероятность нахождения частицы (dP) в элементарном объеме (dV) пропорциональна квадрату волновой функции: dP = Y2(x, y, z)× dV. Величина Вероятность нахождения частицы в каком-либо конечном объеме V равна интегралу квадрата волновой функции по данному объему:
Вероятность должна выражаться действительным положительным числом, меньшим или равным единице. Сама же волновая функция может быть положительной, отрицательной или мнимой, поэтому в общем виде используется не квадрат волновой функции, а квадрат ее модуля. Такое толкование физического смысла волновой функции является одним из постулатов квантовой механики. Правомерность такой интерпретации подтверждается соответствием экспериментально определенного взаимного расположения атомов в молекулах и квантово-механического расчета. Из условия, что вероятность события не может быть больше единицы, следует принцип нормирования волновых функций. Вероятность нахождения частицы во всем рассматриваемом объеме должна быть равна единице (частица находится в этом объеме – событие достоверное):
А – нормирующий множитель, коэффициент, входящий в волновую функцию, который подбирается таким образом, чтобы выполнялось условие нормировки.
|

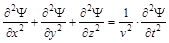 ,
, 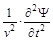 ,
,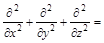 Ñ 2 – оператор Лапласа (читается " набла два").
Ñ 2 – оператор Лапласа (читается " набла два").  .
.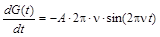 ,
,
 , и соответственно
, и соответственно 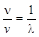 , то
, то .
.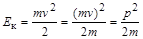 ,
, ,
, 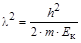
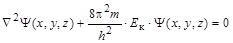 .
.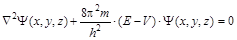 .
. называется плотностью вероятности и характеризует вероятность нахождения частицы в элементарном объеме пространства с координатами x, y, z. Для электрона ее часто называют электронной плотностью.
называется плотностью вероятности и характеризует вероятность нахождения частицы в элементарном объеме пространства с координатами x, y, z. Для электрона ее часто называют электронной плотностью.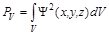 .
.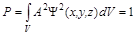 ,
,


