Энергия электрона в трехмерном потенциальном ящике квантована

2. Каждое энергетическое состояние электрона определяется набором из трех квантовых чисел.

Однако в реальных системах часто встречается ситуация, когда определенное энергетическое состояние (энергия частицы) может быть описано не единственным набором квантовых чисел, то есть более чем одной волновой функцией. Тогда говорят о вырождении энергетического состояния.

Проиллюстрировать явление вырождения по энергии можно на примере частицы в трехмерном потенциальном ящике. Если рассмотреть энергетические состояния частицы в ящике, который представляет собою куб (а = b = c), то выражение для энергии приобретает вид

а – параметр куба (величина ребра).

Составим энергетическую диаграмму состояния частицы в таком ящике, откладывая по вертикальной оси энергию частицы в единицах 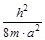(рис.1.5).

Рис. 1.5. Энергетическая диаграмма электрона в трехмерном потенциальном ящике:

[ n_x, n_y, n_z ] – набор квантовых чисел, соответствующий данному энергетическому состоянию

В кубическом потенциальном ящике почти все энергетические состояния в той или иной степени вырождены. Степень вырождения - это число вариантов наборов квантовых чисел (число волновых функций), при помощи которых можно описать данное энергетическое состояние. Снятие вырождения является важной проблемой квантово-механического описания системы. В случае трехмерного потенциального ящика вырождение снимается частично (a = b ¹ c) или полностью (a ¹ b ¹ c) при изменении параметров ящика. В реальных системах проблема снятия вырождения является более сложной проблемой.

Энергетическое состояние электрона в кулоновском поле ядра достаточно близко соответствует ситуации нахождения электрона в трехмерном потенциальном ящике. Поэтому все закономерности, которые были получены, а главное дискретность энергетических состояний, распространяются и на атом.