Основное состояние атома водорода
Атом водорода представляет собой систему, состоящую из положительно заряженного ядра (протон – единичный положительный заряд + e) и одного электрона (единичный отрицательный заряд – e), то есть электрон находится в кулоновском поле положительного заряда (рис. 1.6). Потенциальная энергия точечного заряда в кулоновском поле определяется выражением
где e – единичный электрический заряд; r – расстояние между электроном и ядром; Тогда уравнение Шредингера для атома водорода принимает вид
Рис. 1.7. Связь между декартовыми (x, y, z) и сферическими координатами (r, q, j): x = r × sinJ× cosj, y = r × sinJ× sinj, z = r × cosJ
В общем виде волновая функция в полярных координатах является функцией трех переменных: Учитывая, что
Проведя аналогичные преобразования для координат y и z, просуммируем три полученных выражения:
Решить уравнение Шредингера значит найти набор возможных волновых функций электрона и соответствующих им значений энергий. Это уравнение, как и любое дифференциальное уравнение, имеет бесчисленное множество решений, но физический смысл имеют лишь некоторые из них. В данном случае волновая функция описывает реальную физическую систему – электрон в атоме водорода – и связана с вероятностью его нахождения в определенной области пространства, поэтому она должна: - быть однозначной – вероятность нахождения электрона в элементарном объеме пространства однозначна; - непрерывной; - конечной – ни в одной из точек пространства не равна бесконечности; - убывать до нуля при увеличении расстояния между электроном и ядром. Для сферически симметричного кулоновского поля одной из функций, удовлетворяющих перечисленным условиям, является функция вида
где А – нормирующий коэффициент, а – постоянная величина, определяемая в ходе решения. Для решения поставленной задачи первую и вторую производные предложенной волновой функции подставляют в уравнение Шредингера, определяют параметр а и значение энергии:
Поскольку
Данное уравнение должно быть справедливым при любых значениях переменной r. А это возможно только в том случае, если левая часть равенства и выражение в скобках в правой части одновременно равны нулю:
Из второго уравнения определяют постоянную величину а:
Определив а, из первого уравнения определяют значение энергии электрона:
Вычисление значения энергии основного состояния электрона в атоме водорода дает величину –13, 6 эВ, которая хорошо совпадает с экспериментально определенной энергией ионизации. Полученное значение также совпадает с энергией электрона, находящегося на первой орбите (n =1) атома водорода по теории Бора. Из принципа нормировки следует, что коэффициент
где
|


 ,
, – константа в законе Кулона.
– константа в законе Кулона.
 Поскольку кулоновское поле сферически симметричное, для упрощения решения целесообразно заменить декартову систему координат полярной, в которой в качестве трех координат используются радиус-вектор r и два угла: q (тета – угол между радиус-вектором и осью z) и j (фи – угол между проекцией радиус-вектора на плоскость xy и осью x) (рис. 1.7).
Поскольку кулоновское поле сферически симметричное, для упрощения решения целесообразно заменить декартову систему координат полярной, в которой в качестве трех координат используются радиус-вектор r и два угла: q (тета – угол между радиус-вектором и осью z) и j (фи – угол между проекцией радиус-вектора на плоскость xy и осью x) (рис. 1.7).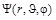 . Поскольку единственный электрон атома водорода находится в сферически симметричном поле ядра, следует ожидать, что решением, описывающим основное (не возбужденное) состояние атома водорода, будет сферически симметричная функция, не зависящая от углов
. Поскольку единственный электрон атома водорода находится в сферически симметричном поле ядра, следует ожидать, что решением, описывающим основное (не возбужденное) состояние атома водорода, будет сферически симметричная функция, не зависящая от углов  .
. , можно произвести замену переменных в уравнении Шредингера. Для этого проводятся следующие математические преобразования:
, можно произвести замену переменных в уравнении Шредингера. Для этого проводятся следующие математические преобразования: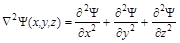 ,
, ,
, ,
, ,
, ,
, .
.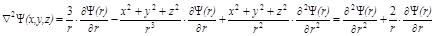 Таким образом, уравнение Шредингера в полярных координатах для основного состояния атома водорода [Y(r)] приобретает следующий вид:
Таким образом, уравнение Шредингера в полярных координатах для основного состояния атома водорода [Y(r)] приобретает следующий вид: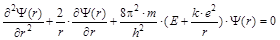 .
. ,
, ,
, 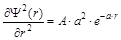 ,
, .
. , то
, то ,
, .
.
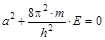 ,
, .
. .
.
 . Тогда волновая функция для основного состояния электрона в атоме водорода имеет вид
. Тогда волновая функция для основного состояния электрона в атоме водорода имеет вид ,
,


