МЕТОДИЧЕСКИЕ УКАЗАНИЯ. Типовой расчет содержит семь заданий
Типовой расчет содержит семь заданий. В заданиях I и II предлагается найти неопределенные интегралы, используя их простейшие свойства, такие, как линейность, и основные приемы интегрирования – замену переменной (или внесение под знак дифференциала) и интегрирование по частям. Напомним указанные свойства. Линейность: 1. 2. Пример 1. Найти Решение. Преобразуя подынтегральное выражение в сумму, и используя свойство линейности интеграла, получим сумму двух табличных интегралов:
Теорема (замена переменной в неопределенном интеграле): Пусть функция
где Формулу (*) можно применять, не вводя явно новой переменной. В общем виде она будет выглядеть следующим образом:
Пример 2. Найти Решение. Первый способ. Приведем пример применения формулы *. Пусть требуется найти интеграл Сделаем замену переменной В нашем интеграле Делая замену Второй способ. Сделаем замену переменной по формуле Тогда
Тогда Замечание. Чтобы доказать равенство ответов, полученных обоими способами, можно во втором ответе избавиться от иррациональности в числителе и вынести показатель степени за знак логарифма:
Одним из основных приемов при поиске первообразной является интегрирование по частям. Формула интегрирования по частям имеет вид
Приведем пример использования формулы.
Пример 3. Найти интеграл Решение. Возьмем Тогда
Замечания. 1. При нахождении функции v находят не все первообразные, а только одну из них, поэтому произвольную постоянную С писать не надо; в примере было 2. Очевидно, основная трудность применения этой формулы состоит в том, чтобы правильно выбрать компоненты интеграла u и dv. Обычно этот метод применяется, когда под знаком интеграла имеется трансцендентная функция, такая как Если же трансцендентность после дифференцирования не исчезает, то эту функцию включают в состав dv, например, в предыдущем примере
|

 .
. .
. .
.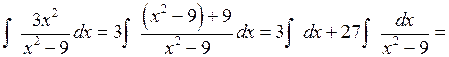
 .
. является первообразной для функции
является первообразной для функции 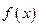 на некотором промежутке
на некотором промежутке 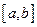 и функция
и функция  непрерывная и имеет непрерывную производную на промежутке
непрерывная и имеет непрерывную производную на промежутке 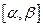 , причем для всякого значения
, причем для всякого значения 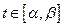 выполняется неравенство
выполняется неравенство  . Тогда будет справедлива формула:
. Тогда будет справедлива формула: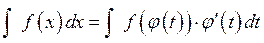 (*),
(*), .
. . Тогда, если
. Тогда, если  - первообразная функции
- первообразная функции  , то
, то 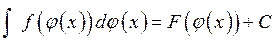 . Такой прием называют внесением под знак дифференциала.
. Такой прием называют внесением под знак дифференциала. ,
,  .
. ,
, 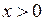 .
. , то есть
, то есть  . Чтобы применить формулу, нужно сделать замену переменной в подынтегральной функции
. Чтобы применить формулу, нужно сделать замену переменной в подынтегральной функции  и положить
и положить  .
. и
и 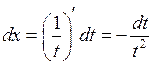 . Тогда
. Тогда 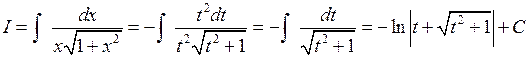 .
.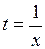 , получим окончательно
, получим окончательно  .
.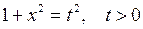 .
.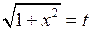 . Для того, чтобы выразить
. Для того, чтобы выразить  через
через  , продифференцируем равенство
, продифференцируем равенство  :
: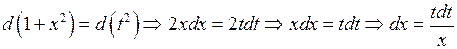 .
.
 .
.
 .
.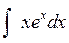 .
. и применим формулу интегрирования по частям. Для этого сначала надо вычислить
и применим формулу интегрирования по частям. Для этого сначала надо вычислить  и v:
и v:  и
и  .
. .
. .
. и т.п. Тогда можно руководствоваться следующим правилом: если производная от трансцендентной функции становится функцией алгебраической (т.е. рациональной или иррациональной дробью), то за u принимается эта функция. Например, в интеграле
и т.п. Тогда можно руководствоваться следующим правилом: если производная от трансцендентной функции становится функцией алгебраической (т.е. рациональной или иррациональной дробью), то за u принимается эта функция. Например, в интеграле  за u надо взять
за u надо взять  , так как
, так как  , то есть после дифференцирования получается дробь.
, то есть после дифференцирования получается дробь. была включена в dv:
была включена в dv:  .
.


