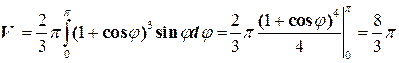В задании VI требуется вычислить длины кривых, заданных тремя различными способами
Если кривая задана в прямоугольной системе координат, уравнением
Если кривая задана параметрическими уравнениями
то длина дуги кривой вычисляется по формуле
Отметим, что здесь, естественно, предполагается, что функции В том случае, когда кривая задана уравнением в полярных координатах
Пример 12. Найти длину дуги кривой Решение. Найдем сначала неопределенный интеграл. Сделаем замену переменной (подстановка Эйлера):
Выразим x через t.
Подставляем в интеграл, учитывая выражение (*) для корня.
Теперь по формуле Ньютона-Лейбница получаем результат:
В задании VII требуется вычислить объем тела, образованного вращением фигуры, ограниченной графиками функций. Причем функция может быть задана в декартовых, параметрических или полярных координатах. Если объем V тела существует и
Объем тела, образованного вращением вокруг оси Ох криволинейной трапеции
Если криволинейная трапеция, ограниченная кривой
Если криволинейный сектор, ограниченный кривой
Рассмотрим типовые задачи: Пример 13. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями Решение. Т.к. область значений функции Найдём абсциссы точек пересечения кривых. Для этого решим систему уравнений:
Имеем Тогда, объем тела:
Пример 14. Фигура, ограниченная кривой Решение. Если t=0, то x=4, y=0, если t=
Пример 15. Фигура, ограниченная линией Решение. Фигура симметрична относительно полярной оси, поэтому для вычисления объема достаточно вращать ее верхнюю половину
|

 , где
, где  , то ее длина находится по формуле
, то ее длина находится по формуле
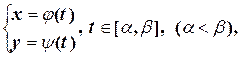

 ,
,  и их производные
и их производные  и
и  непрерывны на промежутке
непрерывны на промежутке  .
. , причём функция
, причём функция  и её производная
и её производная  непрерывны на промежутке
непрерывны на промежутке  , то
, то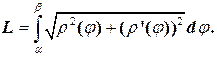


 (*)
(*)





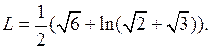
 есть площадь сечения тела плоскостью, перпендикулярной к оси Ох в точке x, то
есть площадь сечения тела плоскостью, перпендикулярной к оси Ох в точке x, то .
.
 , где
, где 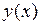 - непрерывная однозначная функция, равен
- непрерывная однозначная функция, равен
 , вращается вокруг оси Оу, то объем тела вращения вычисляется по формуле:
, вращается вокруг оси Оу, то объем тела вращения вычисляется по формуле: .
. и лучами
и лучами  вращается вокруг полярной оси, то объем тела вращения равен:
вращается вокруг полярной оси, то объем тела вращения равен:
 и
и  .
. -
- 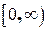 , то фигура, ограниченная заданными линиями будет лежать в верхней полуплоскости.
, то фигура, ограниченная заданными линиями будет лежать в верхней полуплоскости.
 ,
,  .
.
 ,
, 
 и осью Ox, вращается вокруг оси Оy. Найти объем тела вращения.
и осью Ox, вращается вокруг оси Оy. Найти объем тела вращения. , то x=0, y=0. Причем
, то x=0, y=0. Причем  и
и  . Следовательно, объем тела вращения равен:
. Следовательно, объем тела вращения равен:
 , вращается вокруг полярной оси. Найти объем тела вращения.
, вращается вокруг полярной оси. Найти объем тела вращения. .
.