В задании IV требуется проинтегрировать некоторую тригонометрическую функцию. Рассмотрим основные приемы вычисления подобных интегралов
1. Интеграл вида Применение этой подстановки доказывает, что каждый интеграл 2. Универсальная тригонометрическая подстановка очень часто приводит к дроби, интегрирование которой представляет собой весьма трудоемкий процесс. Поэтому эта подстановка на практике используется очень редко. Чаще при вычислении интеграла вида а) Если функция b) Если функция c) Если функция 3. Интегралы вида 4. Рассмотрим интегралы вида Если n – нечетное число, то можно сделать подстановку Если оба показателя n и m четные, то применяют формулы понижения степени: 5. Некоторые интегралы от рациональных и иррациональных функций легко вычисляются с помощью тригонометрических подстановок, в частности: - интеграл вида - интеграл вида - интеграл вида - интеграл вида
Рассмотрим несколько примеров. Пример 6. Найти интеграл Решение. Применим универсальную тригонометрическую подстановку*: Тогда
Пример 7. Найти интеграл Решение. Функция, стоящая под интегралом, нечетна относительно синуса:
Пример 8. Найти интеграл Решение. Преобразуем произведение, стоящее под знаком интеграла в сумму:
Пример 9. Найти интеграл Решение. Так как
Пример 10. Вычислить интеграл Решение. Здесь
|

 , где
, где 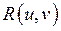 - рациональная функция, можно привести к интегралу от рациональной дроби универсальной тригонометрической подстановкой
- рациональная функция, можно привести к интегралу от рациональной дроби универсальной тригонометрической подстановкой  . Используя формулы тригонометрии, получим
. Используя формулы тригонометрии, получим  . Кроме того
. Кроме того  , откуда
, откуда  .
. , стоящей под интегралом, выражается через элементарные функции.
, стоящей под интегралом, выражается через элементарные функции. - рациональная функция двух переменных, применяются следующие подстановки:
- рациональная функция двух переменных, применяются следующие подстановки: нечетна относительно первой переменной, т.е.
нечетна относительно первой переменной, т.е.  , то применяется подстановка
, то применяется подстановка  .
. , то применяется подстановка
, то применяется подстановка  .
.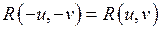 , то применяется подстановка
, то применяется подстановка  .
. ,
,  и
и  приводятся к табличным с помощью формул преобразования произведения тригонометрических функций в сумму.
приводятся к табличным с помощью формул преобразования произведения тригонометрических функций в сумму. , где n и m – целые неотрицательные числа.
, где n и m – целые неотрицательные числа. . Тогда
. Тогда  ,
,  и данный интеграл приводится к виду
и данный интеграл приводится к виду 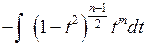 . Если n – число четное, но нечетным будет m, то аналогично можно сделать подстановку
. Если n – число четное, но нечетным будет m, то аналогично можно сделать подстановку  и привести интеграл к виду
и привести интеграл к виду  .
. .
. можно вычислить с помощью подстановки
можно вычислить с помощью подстановки  ;
; можно вычислить с помощью подстановки
можно вычислить с помощью подстановки  ;
; можно вычислить с помощью подстановки
можно вычислить с помощью подстановки 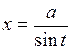 ;
;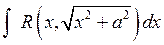 можно вычислить с помощью подстановки
можно вычислить с помощью подстановки  .
. .
. .
. .
. , поэтому сделаем подстановку
, поэтому сделаем подстановку  . Тогда
. Тогда
 .
. .
. .
. стоит в нечетной степени, то сделаем замену
стоит в нечетной степени, то сделаем замену  . Тогда
. Тогда .
. .
.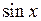 стоит в четной степени, поэтому воспользуемся формулами понижения степени:
стоит в четной степени, поэтому воспользуемся формулами понижения степени:



