В задании III требуется найти интеграл от рациональной функции. Опишем указанную процедуру, приведя основную теорему
1. Рациональной дробью называется выражение вида Например, дроби 2. Рациональная дробь называется правильной, если степень многочлена, стоящего в числителе, строго меньше степени многочлена, стоящего в знаменателе. В противном случае дробь называется неправильной. В предыдущих примерах первая дробь будет правильной, а две последние неправильными. 3. Простейшими дробями будем называть дроби вида Если дробь неправильная, то из нее можно выделить целую часть, то есть представить дробь в виде Правильную дробь всегда можно представить в виде суммы простейших дробей.
Теорема о разложении правильной рациональной дроби в сумму простейших дробей. Пусть дробь
Замечание. Теорема утверждает, что каждая правильная дробь раскладывается на сумму простейших дробей в соответствии с разложением на множители знаменателя. Каждому множителю вида Рассмотрим теперь интеграл Чтобы его вычислить, достаточно руководствоваться несколькими правилами: 1) Если дробь 2) Правильную дробь надо разложить на сумму простейших дробей. Тогда интеграл от этой дроби сведется к сумме интегралов от простейших дробей. Как нам известно*, простейшие дроби бывают четырех типов:
Интегрирование третьей дроби мы уже рассматривали*. Рассмотрим интегрирование простейшей дроби четвертого типа. Сначала выделим полный квадрат в знаменателе этой дроби: где
Что касается второго интеграла, то к нему применяется прием, называемый понижением степени. Обозначим этот интеграл через
и разобьем его на два слагаемых Последний интеграл проинтегрируем по частям, положив Тогда Откуда
Окончательно получим
Формула В дальнейшем мы узнаем еще один способ вычисления подобного интеграла.
Рассмотрим несколько примеров. Пример 4. Вычислить Решение. Дробь, стоящую под знаком интеграла, представим в виде суммы простейших дробей с неопределенными коэффициентами: 1) Два многочлена равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях. 2) Два многочлена равны тогда и только тогда, когда значения этих многочленов равны при любом значении переменной х. В этом примере воспользуемся первым критерием равенства многочленов. Раскрывая скобки, получим Тогда Пример 5. Вычислить Решение. Дробь, стоящая под интегралом, неправильная, поэтому из нее надо выделить целую часть. Это можно сделать делением числителя на знаменатель уголком
Отсюда
Дробь, стоящую в последнем интеграле, разложим на простейшие: Откуда
Подставляя в первое равенство
из которой окончательно находим все коэффициенты: Вернемся к интегралу от правильной дроби:
В последнем интеграле выделим полный квадрат в знаменателе
|

 , где
, где  и
и  многочлены от переменной х степени n и m соответственно.
многочлены от переменной х степени n и m соответственно. ,
, 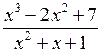 ,
,  являются рациональными дробями относительно переменной х.
являются рациональными дробями относительно переменной х.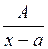 ,
,  ,
,  и
и  , где дискриминант квадратного трехчлена, стоящего в знаменателях двух последних дробей, строго меньше нуля, то есть эти знаменатели нельзя разложить на вещественные простые множители.
, где дискриминант квадратного трехчлена, стоящего в знаменателях двух последних дробей, строго меньше нуля, то есть эти знаменатели нельзя разложить на вещественные простые множители. , где
, где  многочлен степени n-m, а
многочлен степени n-m, а  - многочлен степени
- многочлен степени 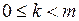 , то есть дробь
, то есть дробь 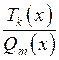 - правильная. Чтобы получить такое представление дроби, надо разделить числитель
- правильная. Чтобы получить такое представление дроби, надо разделить числитель  разложен на множители в области вещественных чисел, то есть
разложен на множители в области вещественных чисел, то есть  , где все квадратные трехчлены
, где все квадратные трехчлены  не имеют вещественных корней. Тогда
не имеют вещественных корней. Тогда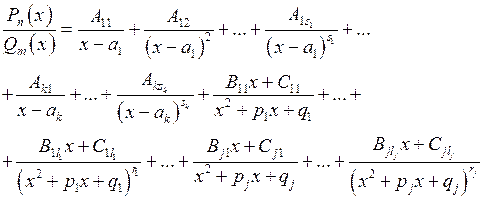 .
. соответствует k дробей вида
соответствует k дробей вида  , где показатель i меняется от 1 до s, и в числителях стоят некоторые константы
, где показатель i меняется от 1 до s, и в числителях стоят некоторые константы 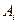 , и каждому множителю вида
, и каждому множителю вида  соответствуют m дробей вида
соответствуют m дробей вида  , где показатель j меняется от 1 до r, а в числителях стоят линейные функции
, где показатель j меняется от 1 до r, а в числителях стоят линейные функции  .
. .
. . Первые две из них интегрируются подведением под знак дифференциала:
. Первые две из них интегрируются подведением под знак дифференциала:
 .
. . Так как дискриминант квадратного трехчлена отрицателен, то
. Так как дискриминант квадратного трехчлена отрицателен, то  , поэтому можно ввести обозначение
, поэтому можно ввести обозначение  . Кроме того, введем замену переменной
. Кроме того, введем замену переменной  . Тогда
. Тогда 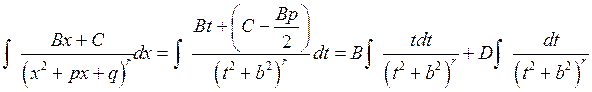 ,
, . Первый из полученных интегралов берется подведением под знак дифференциала:
. Первый из полученных интегралов берется подведением под знак дифференциала: .
. . Сначала преобразуем числитель этого интеграла
. Сначала преобразуем числитель этого интеграла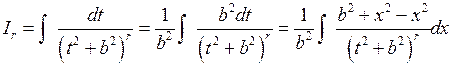
 .
. .
. ,
, .
.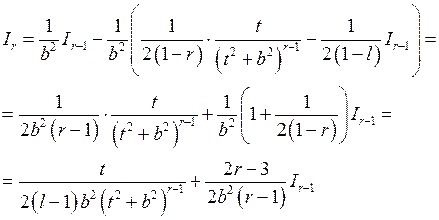
 называется рекуррентной формулой и ею можно пользоваться при вычислении подобных интегралов, но так как эту формулу трудно выучить наизусть, предпочтительнее при вычислении таких интегралов пользоваться тем приемом, с помощью которого эта формула была получена.
называется рекуррентной формулой и ею можно пользоваться при вычислении подобных интегралов, но так как эту формулу трудно выучить наизусть, предпочтительнее при вычислении таких интегралов пользоваться тем приемом, с помощью которого эта формула была получена. .
. . Чтобы найти коэффициенты разложения, снова приведем сумму этих простейших к общему знаменателю. Тогда
. Чтобы найти коэффициенты разложения, снова приведем сумму этих простейших к общему знаменателю. Тогда  . Сравним первую дробь этого равенства с последней. Так как знаменатели этих дробей равны, то должны быть равны и числители, т. е.
. Сравним первую дробь этого равенства с последней. Так как знаменатели этих дробей равны, то должны быть равны и числители, т. е.  . Теперь для нахождения неопределенных коэффициентов можно воспользоваться одним из двух критериев равенства двух многочленов:
. Теперь для нахождения неопределенных коэффициентов можно воспользоваться одним из двух критериев равенства двух многочленов: . В многочленах справа и слева приравняем коэффициенты при х и свободные члены. Получится система
. В многочленах справа и слева приравняем коэффициенты при х и свободные члены. Получится система  , решая которую, находим А=3 и В=-2.
, решая которую, находим А=3 и В=-2. .
. .
.
 и
и 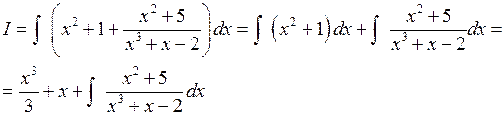 .
. ,
, и
и  .
. , получим
, получим  или
или  . Из второго равенства получаем систему
. Из второго равенства получаем систему ,
, .
.
 и сделаем замену переменной
и сделаем замену переменной 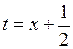 . Тогда
. Тогда  . Окончательно,
. Окончательно,



