Если область  ограничена сверху кривой
ограничена сверху кривой  , снизу кривой
, снизу кривой  , причём
, причём  , то площадь области
, то площадь области  можно вычислить по формуле
можно вычислить по формуле
 , т.е.
, т.е. 
Если кривая задана параметрически  и при изменении параметра
и при изменении параметра  точка пробегает кривую L, лежащую выше оси OX от
точка пробегает кривую L, лежащую выше оси OX от  до
до  , то площадь криволинейной трапеции, ограниченной данной кривой, осью абсцисс и прямыми
, то площадь криволинейной трапеции, ограниченной данной кривой, осью абсцисс и прямыми  и
и  находится по формуле
находится по формуле  По той же формуле можно найти и площадь фигуры, ограниченной замкнутой кривой L, заданной параметрически и пробегаемой по часовой стрелке,. При этом
По той же формуле можно найти и площадь фигуры, ограниченной замкнутой кривой L, заданной параметрически и пробегаемой по часовой стрелке,. При этом  соответствуют значениям параметра, при которых кривая замыкается.
соответствуют значениям параметра, при которых кривая замыкается.
Пример 11. Вычислить площадь фигуры, ограниченной кривыми 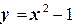 и
и  .
.
Решение.







 Найдём точки пересечения данных кривых. Для этого необходимо решить систему уравнений
Найдём точки пересечения данных кривых. Для этого необходимо решить систему уравнений


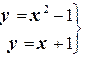


Решив её, найдём координаты точек
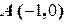
и
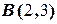
. Тогда, очевидно, что площадь фигуры
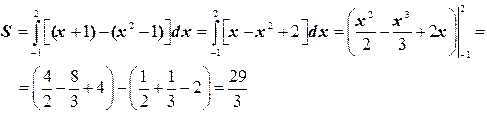
Кривая, ограничивающая область, может быть задана в полярных координатах. Точнее, рассмотрим площадь фигуры, ограниченной лучами  , а также кривой
, а также кривой  (предполагаем, естественно, что функция
(предполагаем, естественно, что функция  на промежутке
на промежутке  интегрируема). Площадь данного криволинейного сектора находится по формуле
интегрируема). Площадь данного криволинейного сектора находится по формуле  .
.
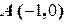 и
и 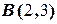 . Тогда, очевидно, что площадь фигуры
. Тогда, очевидно, что площадь фигуры

 ограничена сверху кривой
ограничена сверху кривой  , снизу кривой
, снизу кривой  , причём
, причём  , то площадь области
, то площадь области  , т.е.
, т.е. 
 и при изменении параметра
и при изменении параметра  точка пробегает кривую L, лежащую выше оси OX от
точка пробегает кривую L, лежащую выше оси OX от  до
до  , то площадь криволинейной трапеции, ограниченной данной кривой, осью абсцисс и прямыми
, то площадь криволинейной трапеции, ограниченной данной кривой, осью абсцисс и прямыми  находится по формуле
находится по формуле  По той же формуле можно найти и площадь фигуры, ограниченной замкнутой кривой L, заданной параметрически и пробегаемой по часовой стрелке,. При этом
По той же формуле можно найти и площадь фигуры, ограниченной замкнутой кривой L, заданной параметрически и пробегаемой по часовой стрелке,. При этом  соответствуют значениям параметра, при которых кривая замыкается.
соответствуют значениям параметра, при которых кривая замыкается.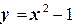 и
и  .
.






 Найдём точки пересечения данных кривых. Для этого необходимо решить систему уравнений
Найдём точки пересечения данных кривых. Для этого необходимо решить систему уравнений
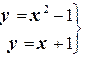



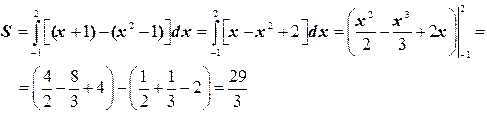
 , а также кривой
, а также кривой  (предполагаем, естественно, что функция
(предполагаем, естественно, что функция  интегрируема). Площадь данного криволинейного сектора находится по формуле
интегрируема). Площадь данного криволинейного сектора находится по формуле  .
.


