Трение скольжения
Для определения коэффициента трения в данной работе используется метод наклонного маятника (рис. 13.1). Шарик или брусок, подвешенные в точке О, опираются на наклонную плоскость, угол наклона которой к горизонту b можно изменять. Если отклонить маятник от положения равновесия на угол a0, то он начнет совершать затухающие колебания. В результате за n колебаний угол отклонения уменьшится до значения
а б Рис. 13.1 Коэффициент трения скольжения
В рассматриваемом случае (рис. 13.1а) сила реакции опоры по модулю равна составляющей силы тяжести
где m – масса маятника, g – ускорение свободного падения. Сила трения может быть найдена с помощью закона сохранения энергии. Согласно которому работа, совершенная силой трения за n колебаний, равна изменению потенциальной энергии тела за то же число колебаний
где С учетом формул (13.2) и (13.3) формула (13.1) принимает вид
Далее, из рис. 13.1б видно, что
где Подставив (13.5) в (13.4), получим для коэффициента трения скольжения формулу
Теперь осталось выразить величины
Если учесть, что при малых углах
Путь S, пройденный телом, можно найти, руководствуясь следующими соображениями. За одно полное колебание тело проходит расстояние, равное четырем амплитудам 4 A. За n колебаний пройденный путь S = 4 nA. Но амплитуда вследствие затухания изменяется от начального значения А 0, равного дуге DF, до конечного значения A n, равного дуге DE, поэтому надо взять ее среднее значение. Из рис. 13.2б видно, что А 0 » a0 L, а A n » an L (здесь углы выражены в радианах), следовательно, среднее значение амплитуды равно L (a0 + an)/2. Итак,
Подставив (13.7) и (13.8) в (13.6), получим формулу для расчета коэффициента трения скольжения в данной работе
|

 . Затухание колебаний происходит главным образом под действием внешнего трения.
. Затухание колебаний происходит главным образом под действием внешнего трения.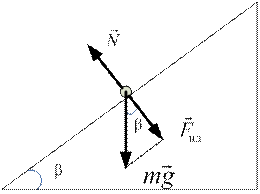

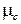 равен отношению силы трения
равен отношению силы трения  к силе реакции опоры N (которая, согласно III закону Ньютона, всегда равна силе нормального давления
к силе реакции опоры N (которая, согласно III закону Ньютона, всегда равна силе нормального давления  , прижимающей тело к опоре)
, прижимающей тело к опоре) . (13.1)
. (13.1) , направленной перпендикулярно плоскости
, направленной перпендикулярно плоскости , (13.2)
, (13.2)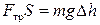 , (13.3)
, (13.3) – работа силы трения, S – расстояние, пройденное телом за n колебаний,
– работа силы трения, S – расстояние, пройденное телом за n колебаний,  – изменение потенциальной энергии тела за то же число колебаний, D h – изменение высоты тела вследствие затухания колебаний.
– изменение потенциальной энергии тела за то же число колебаний, D h – изменение высоты тела вследствие затухания колебаний.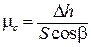 . (13.4)
. (13.4) , (13.5)
, (13.5) – расстояние между начальным и конечным положениями тела, отсчитанное по наклонной плоскости.
– расстояние между начальным и конечным положениями тела, отсчитанное по наклонной плоскости.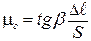 . (13.6)
. (13.6) через величины, измеряемые на опыте: число колебаний и углы отклонения маятника от положения равновесия
через величины, измеряемые на опыте: число колебаний и углы отклонения маятника от положения равновесия  и
и 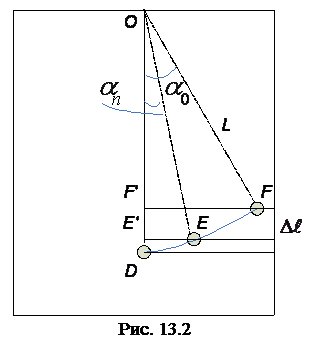 На рисунке изображены три положения тела: положение равновесия D, начальное положение F, соответствующее отклонению на угол
На рисунке изображены три положения тела: положение равновесия D, начальное положение F, соответствующее отклонению на угол  .
.  и
и  можно представить через длину нити маятника L и углы его отклонения от положения равновесия. Действительно, из треугольника EOE ¢ следует, что
можно представить через длину нити маятника L и углы его отклонения от положения равновесия. Действительно, из треугольника EOE ¢ следует, что  , а из треугольника FOF¢ –
, а из треугольника FOF¢ –  . Итак,
. Итак,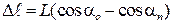 .
. то
то 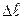 можно представить в виде
можно представить в виде . (13.7)
. (13.7) . (13.8)
. (13.8)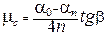 . (13.9)
. (13.9)


