Свободные оси вращения.Главные оси инерции
В данной работе рассматривается вращение твердого тела вокруг неподвижной оси (рис. 14.1). При таком движении все точки тела движутся в параллельных плоскостях по концентрическим окружностям, центры которых лежат на одной прямой, называемой осью вращения ОО (рис. 14.1). Основной закон динамики для тела, вращающегося относительно неподвижной оси, записывается в виде
где Момент инерции тела относительно оси его вращения может быть определен по формулам (Т.10) или (Т. 11):
где Первая формула предпочтительна для системы дискретных тел, вторая – для сплошных тел.
Чтобы пояснить, что такое свободные оси, рассмотрим простейшую систему тел, состоящую из двух тел одинаковой массы Если же ось вращения проходит через центр масс системы ² стержень – массы² и при этом является осью ее симметрии (рис.14.2б), то силы, действующие на стержень со стороны вращающихся тел, направлены по одной прямой и, следовательно, уравновешивают друг друга.
Это значит, что стержень не действует на ось, а она – на подшипники. Если подшипники убрать, ось этого ² не заметит², она будет сохранять свое направление в пространстве. Конечно, под действием силы тяжести система будет падать, но при этом будет продолжать вращаться в горизонтальной плоскости вокруг вертикальной оси. Такие оси, которые сами (без действия внешних сил) сохраняют неизменным свое направление в пространстве, называются свободными осями вращения.
Две из трех главных осей инерции, а именно те, относительно которых момент инерции максимален и минимален ( на рис. это оси Х и Z ), являются устойчивыми. Третья ось, относительно которой момент инерции имеет среднее значение, – неустойчива. Ось устойчива – это значит, что при небольших случайных отклонениях вращения от этой оси возникают силы, возвращающие тело к вращению вокруг этой оси. Следовательно, в отсутствие сил сопротивления вращение вокруг устойчивых осей продолжалось бы бесконечно долго. Но силы сопротивления всегда имеют место, поэтому для поддержания вращения даже вокруг главных осей необходимо прикладывать момент внешних сил, хотя и много меньший, чем при вращении вокруг других осей. В таком случае обычно устойчивой оказывается одна главная ось, а именно та, относительно которой момент инерции имеет максимальное значение. Для того чтобы машина служила долго, вращающимся частям придают форму, возможно более близкую к телам вращения, а ось как можно точнее совмещают с главной осью инерции. Однако совместить абсолютно точно ось вращения с главной осью инерции тела практически невозможно, поэтому для быстро вращающихся частей машин применяют гибкие, самоцентрирующиеся оси.
|

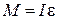 , (14.1)
, (14.1)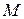 – результирующий момент всех внешних сил,
– результирующий момент всех внешних сил, 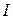 – момент инерции тела относительно оси вращения,
– момент инерции тела относительно оси вращения,  –угловое ускорение тела.
–угловое ускорение тела. ,
,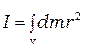 , (14.2)
, (14.2)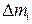 – масса малого объема тела, все точки которого можно считать удаленными от оси вращения на одинаковое расстояние
– масса малого объема тела, все точки которого можно считать удаленными от оси вращения на одинаковое расстояние 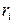 ,
, 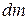 – элементарная масса, V – объем тела.
– элементарная масса, V – объем тела.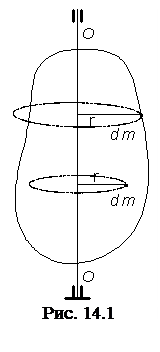 Из (14.2) следует, что момент инерции зависит от распределения массы тела относительно оси его вращения. Очевидно, что осей вращения может быть бесконечно много. Но среди всех осей особое значение имеют оси, называемые свободными осями вращения. Свободные оси вращения – это такие оси, которые сами (без действия внешних сил) могут сохранять свое направление в пространстве неизменным.
Из (14.2) следует, что момент инерции зависит от распределения массы тела относительно оси его вращения. Очевидно, что осей вращения может быть бесконечно много. Но среди всех осей особое значение имеют оси, называемые свободными осями вращения. Свободные оси вращения – это такие оси, которые сами (без действия внешних сил) могут сохранять свое направление в пространстве неизменным.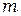 , закрепленных на жестком невесомом стержне
, закрепленных на жестком невесомом стержне  (рис. 14.2). Стержень в свою очередь закреплен в точке С, являющейся центром масс системы, на вертикальной оси ОО, которая может вращаться в подшипниках П 1 и П 2. Пусть стержень составляет с осью некоторый угол (рис. 14.2а). При вращении системы ² стержень – массы² на концы стержня со стороны масс действуют силы
(рис. 14.2). Стержень в свою очередь закреплен в точке С, являющейся центром масс системы, на вертикальной оси ОО, которая может вращаться в подшипниках П 1 и П 2. Пусть стержень составляет с осью некоторый угол (рис. 14.2а). При вращении системы ² стержень – массы² на концы стержня со стороны масс действуют силы 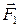 и
и  . Вследствие того, что тела расположены несимметрично относительно оси вращения, силы
. Вследствие того, что тела расположены несимметрично относительно оси вращения, силы 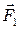 и
и  не лежат на одной прямой и создают момент пары сил, стремящийся повернуть ось, придать ей горизонтальное направление. Чтобы ось удерживалась в неизменном положении, подшипники должны действовать на нее с силами
не лежат на одной прямой и создают момент пары сил, стремящийся повернуть ось, придать ей горизонтальное направление. Чтобы ось удерживалась в неизменном положении, подшипники должны действовать на нее с силами  и
и 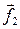 . Таким образом, ось остается неподвижной только благодаря подшипникам. Если убрать подшипники, ось вращения поменяет свое направление в пространстве. В рассматриваемом примере быстро изнашиваются и ось, и подшипники.
. Таким образом, ось остается неподвижной только благодаря подшипникам. Если убрать подшипники, ось вращения поменяет свое направление в пространстве. В рассматриваемом примере быстро изнашиваются и ось, и подшипники.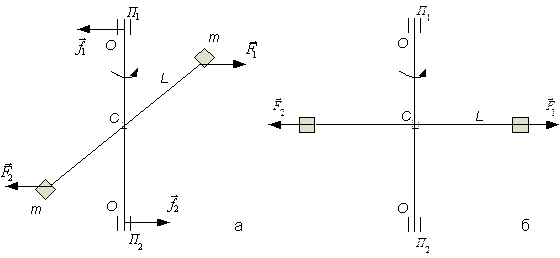 Рис. 14.2
Рис. 14.2
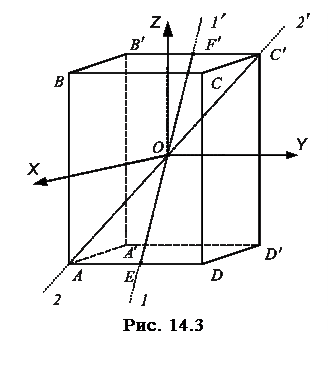 Также обстоит дело с телом какой угодно формы. Теоретически доказывается, что в нем всегда существуют такие три взаимно перпендикулярные оси, проходящие через центр тяжести тела (он же центр масс, или центр инерции), которые могут служить свободными осями вра-щения. Они называются главными осями инерции. Для тел пра-вильной формы эти оси инерции легко могут быть найдены. Например, главными осями инерции прямоугольного параллеле-пипеда являются оси X, Y, Z (рис. 14.3), проведенные через центры противоположных граней.
Также обстоит дело с телом какой угодно формы. Теоретически доказывается, что в нем всегда существуют такие три взаимно перпендикулярные оси, проходящие через центр тяжести тела (он же центр масс, или центр инерции), которые могут служить свободными осями вра-щения. Они называются главными осями инерции. Для тел пра-вильной формы эти оси инерции легко могут быть найдены. Например, главными осями инерции прямоугольного параллеле-пипеда являются оси X, Y, Z (рис. 14.3), проведенные через центры противоположных граней.


