Описание установки и метода измерений
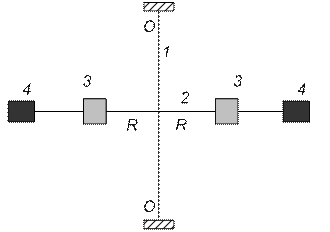
Установка для определения скорости полета пули (рис. 12.1) состоит из основания с вертикальной стойкой с тремя кронштейнами, крутильного маятника и пускового устройства. Измерительным прибором является баллистический крутильный маятник (рис. 12.2). Он выполнен в виде стержня 2, на концах которого имеются мишени 4 с пластилином. По стержню могут перемещаться грузы 3. Упругая стальная проволока 1, на которой закреплен стержень, совпадает с осью вращения крутильного маятника ОО. Перемещающиеся грузы 3 служат для изменения момента инерции маятника. Пусковое устройство заряжается ″ пулей″, после чего производится ″ выстрел″ по мишени маятника. Максимальный угол отклонения стержня при этом ″ выстреле″ fmax определяется по шкале, нанесенной на кожухе. Принцип работы установки основан на зависимости максимального угла отклонения маятника от скорости полета ″ пули″. После того, как будет произведен ″ выстрел″ и ″ пуля″ прилипнет к мишени, маятник начнет совершать крутильные колебания, период которых зависит от момента инерции маятника и от упругих свойств подвеса. Систему ² маятник – пуля² можно считать изолированной, и следова-тельно, для нее можно записать закон сохранения момента импульса. Так как удар пули о мишень является абсолютно неупругим (пуля прилипает к мишени), закон сохранения момента импульса для системы ² маятник–пуля² имеет вид
где m – масса пули,
Рис. 12.1
Рис. 12.2
Период колебаний маятника Поскольку момент инерции пули
В уравнении (12.2) три неизвестные величины: скорость пули В качестве одного из уравнений используем закон сохранения механической энергии. Если пренебречь сопротивлением воздуха, то кинетическая энергия маятника сразу после попадания в него пули равна потенциальной энергии закрученной упругой стальной проволоки:
где D – коэффициент жесткости проволоки, В качестве второго уравнения используем формулу периода крутильных колебаний (вывод см. в работе 1.3):
Из (12.4) после возведения его в квадрат выражают коэффициент D, который затем подставляют в (12.3) и получают выражение для начальной угловой скорости
В формуле (12.5) все величины легко измеряются на опыте, кроме момента инерции маятника I, который складывается из момента инерции всех частей маятника за исключением момента инерции перемещающихся грузов и момента инерции перемещающихся грузов. Передвигая грузы 3 вдоль стержня можно изменять момент инерции маятника. Запишем формулу момента инерции маятника для случаев, когда центры грузов находятся на расстояниях
где Непосредственно из системы уравнений (12.6), в которой три неизвестных, нельзя найти ни I 1, ни I 2, а можно найти только их разность
Для нахождения самих моментов инерции вновь используют (12.4). Записывают (12.4) для двух положений грузов, соответствующих моментам инерции I 1 и I 2,
Затем, представив в (12.8) один момент инерции через другой, например
Подставив (12.9) с учетом (12.7) в (12.5), получают формулу для расчета скорости пули в данной работе
где
|

 , (12.1)
, (12.1)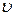 – скорость ее движения,
– скорость ее движения, 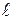 – расстояние от точки попадания пули в мишень до оси вращения маятника ОО,
– расстояние от точки попадания пули в мишень до оси вращения маятника ОО,  – начальная угловая скорость маятника,
– начальная угловая скорость маятника, 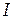 – момент инерции маятника относительно оси вращения.
– момент инерции маятника относительно оси вращения.
 можно определить на опыте, измерив с помощью секундомера время
можно определить на опыте, измерив с помощью секундомера время  , за которое совершается
, за которое совершается 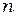 колебаний,
колебаний,  .
.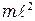 пренебрежимо мал по сравнению с моментом инерции маятника, то им в (12.1) можно пренебречь и искомую скорость пули представить, как
пренебрежимо мал по сравнению с моментом инерции маятника, то им в (12.1) можно пренебречь и искомую скорость пули представить, как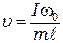 . (12.2)
. (12.2) , (12.3)
, (12.3) – максимальный угол отклонения маятника.
– максимальный угол отклонения маятника. . (12.4)
. (12.4) . (12.5)
. (12.5) и
и 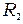 от оси вращения:
от оси вращения: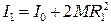 ,
, , (12.6)
, (12.6) – момент инерции всех частей маятника за исключением момента инерции подвижных грузов,
– момент инерции всех частей маятника за исключением момента инерции подвижных грузов, 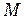 – масса одного подвижного груза.
– масса одного подвижного груза. ,
,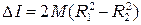 . (12.7)
. (12.7)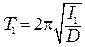 ,
, . (12.8)
. (12.8)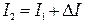 , получают
, получают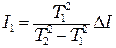 . (12.9)
. (12.9)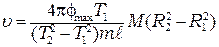 , (12.10)
, (12.10) ,
, 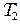 , fmax и
, fmax и 


