Порядок выполнения работы. 1. Определить длину математического маятника (измеряется от уровня закрепления до центра масс маятника)1. Определить длину математического маятника 2. Отклонить маятник на 10–15° и отпустить. Определить время 15–30 полных колебаний. Повторить опыт 3 раза. 3. Найти среднее время n колебаний и период колебаний маятника 4. По средним значениям длины и периода по формуле (10.11) вычислить ускорение свободного падения в данной точке Земли. 5. Данные занести в таблицу
6. Оценить погрешность полученного значения g методом косвенных измерений, предварительно оценив методом прямых измерений погрешности длины и периода. Формулу для расчета погрешности g получить, воспользовавшись формулой (П.7) из параграфа ² Расчет погрешностей…². Контрольные вопросы 1. Какая сила называется силой тяжести? Почему она отличается от силы тяготения? Запишите закон всемирного тяготения. 2. Запишите формулу центробежной силы инерции. Как она направлена и как ее модуль изменяется с широтой. 3. Какая сила заставляет математический маятник колебаться? Запишите для него II закон Ньютона в интегральной и дифференциальной форме. 4. Запишите уравнение гармонического колебательного движения. Как найти скорость и ускорение колеблющейся точки? 5. Что называется амплитудой и периодом колебаний? Как связаны период и циклическая частота? 6. Докажите, что функция (10.8) является решением уравнения (10.7). 7. Дайте вывод расчётной формулы (10.11). ВариантII
|
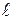(измеряется от уровня закрепления до центра масс маятника).
