Описание установки и метода измерений. Физическим маятником является любое реальное тело (рис
Физическим маятником является любое реальное тело (рис. 10.4), закрепленное на оси О, не проходящей через его центр масс С. Чтобы понять, как движется физический маятник, надо записать для него основной закон динамики вращательного движения (II закон Ньютона для вращательного движения)
где М – момент силы, действующий на маятник, I – момент инерции маятника относительно оси вращения, e – его угловое ускорение. Когда маятник отклонен от положения равновесия на угол a, его силу тяжести
Подставив (10.14) в (10.13) получают II закон Ньютона для маятника в виде
где m – масса маятника, g – ускорение свободного падения, знак ² –² показывает, что момент силы возвращает маятник в положение равновесия. Так как синусы (и тангенсы) малых углов примерно равны самим углам в радианах (т. е. sina = a), а угловое ускорение равно второй производной от угла отклонения по времени (т. е.
В (10.16) все величины, кроме угла a, постоянны, поэтому можно ввести обозначение
и записать (10.17) в виде
Решив дифференциальное уравнение (10.186), находят, что угол отклонения маятника от положения равновесия a является следующей функцией времени (в этом можно убедиться путем подстановки):
Итак, при малых углах отклонения маятник движется по закону косинуса (или синуса), другими словами, маятник совершает гармоническое колебательное движение. Анализ уравнения (10.19) показывает, что amax и j0 – амплитуда и начальная фаза колебаний, а w0 – циклическая частота, связанная с периодом колебаний соотношением
откуда с учетом (10.17)
С помощью формулы (10.21) можно определить ускорение свободного падения, если известен момент инерции маятника относительно оси вращения. Момент инерции маятника I относительно оси О можно представить с помощью теоремы Штейнера
где С учетом (10.22) формула (10.21) принимает вид
Массу маятника и период его колебаний можно измерить на опыте с очень высокой точностью, но точно измерить момент инерции
где Исключив
Все величины в (10.25) легко измеряются на опыте. Периоды колебаний находят по (10.12), определив время 20–30 полных колебаний. Для определения
|

 , (10.13)
, (10.13) , приложенную в центре масс С, можно разложить на две составляющие:
, приложенную в центре масс С, можно разложить на две составляющие:  , направленную вдоль прямой ОС, и
, направленную вдоль прямой ОС, и  , перпендикулярную к ней. Составляющая силы тяжести
, перпендикулярную к ней. Составляющая силы тяжести  , а ее плечо равно
, а ее плечо равно 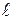 – расстоянию от оси вращения до центра масс. Следовательно, момент силы
– расстоянию от оси вращения до центра масс. Следовательно, момент силы 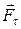 относительно оси вращения равен
относительно оси вращения равен
 . (10.14)
. (10.14) , (10.15)
, (10.15)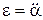 ), то при малых отклонениях (10.15) принимает вид
), то при малых отклонениях (10.15) принимает вид . (10.16)
. (10.16) (10.17)
(10.17) . (10.18)
. (10.18)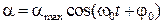 . (10.19)
. (10.19) , (10.20)
, (10.20)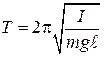 . (10.21)
. (10.21) , (10.22)
, (10.22) – момент инерции маятника относительно оси, проходящей через его центр масс С параллельно оси О.
– момент инерции маятника относительно оси, проходящей через его центр масс С параллельно оси О.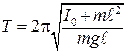 . (10.23)
. (10.23)
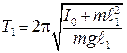 ,
, , (10.24)
, (10.24) – расстояние от оси О 1 до центра масс маятника,
– расстояние от оси О 1 до центра масс маятника,  – расстояние от оси вращения О 2 до центра масс маятника.
– расстояние от оси вращения О 2 до центра масс маятника. . (10.25)
. (10.25) и
и  , наоборот, близки, то для получения достаточно точного значения g нет необходимости определять
, наоборот, близки, то для получения достаточно точного значения g нет необходимости определять 


