Основной закон динамики для вращательного движения в данной работе удобно записать в виде
где М – вращающий момент, действующий на маятник, I – момент инерции маятника, e – угловое ускорение маятника. Из (11.1) следует, что при неизменном моменте сил угловое ускорение маятника обратно пропорционально моменту инерции, т. е. должно выполняться соотношение
Найти отношение моментов инерции на опыте трудно по следующей причине. Момент инерции маятника складывается из момента инерции шкивов с крестовиной I0 и из моментов инерции четырех грузиков
Момент инерции каждого грузика определяется по теореме Штейнера
где
В (11.5) два первых слагаемых не изменяются при изменении расстояния грузиков от оси вращения. Когда грузики находятся на расстоянии
когда грузики находятся на расстоянии
Но I 0 и В работе предлагается другой путь проверки закона (11.1). А именно: предлагается найти не отношение моментов инерции маятника, а их разность теоретически и экспериментально, а затем сравнить полученные значения. Теоретически разность моментов инерции маятника находят, вычтя из уравнения (11.6) уравнение (11.7)
Экспериментально разность моментов инерции маятника можно найти, используя формулу (11.1)
Силами трения в этой работе пренебрегают, поэтому вращающий момент создается только силой натяжения нити
Выразив силу натяжения из (11.10), получают для вращающего момента формулу
Ускорение груза а можно найти из формулы равноускоренного движения
Поскольку нить нерастяжима, то ускорение всех ее точек и любой точки обода шкива радиуса R равно ускорению груза а. Следовательно, угловое ускорение крестовины можно найти по формуле
Подставив (11.11), а также (11.13) с учетом (11.12), в (11.9) (при этом в (11.11) пренебрегают ускорением
Очевидно, что доказательством правильности закона (11.1) является равенство (11.8) и (11.14), т. е. выполнение тождества
где Итак, если при перемещении грузиков
|

 , (11.1)
, (11.1) , или
, или  . (11.2)
. (11.2)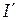 :
: . (11.3)
. (11.3)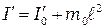 , (11.4)
, (11.4)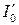 – момент инерции грузика относительно оси симметрии, проходящей через центр масс грузика параллельно оси вращения маятника. Подставив (11.4) в (11.3), получим формулу
– момент инерции грузика относительно оси симметрии, проходящей через центр масс грузика параллельно оси вращения маятника. Подставив (11.4) в (11.3), получим формулу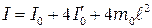 . (11.5)
. (11.5) от оси вращения, момент инерции маятника
от оси вращения, момент инерции маятника , (11.6)
, (11.6) от оси вращения, момент инерции
от оси вращения, момент инерции . (11.7)
. (11.7) . (11.8)
. (11.8) . (11.9)
. (11.9) . Которую находят, рассмотрев движение груза m. II закон Ньютона для него в векторной и скалярной форме имеет вид соответственно
. Которую находят, рассмотрев движение груза m. II закон Ньютона для него в векторной и скалярной форме имеет вид соответственно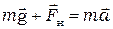 ,
, . (11.10)
. (11.10) . (11.11)
. (11.11) , откуда
, откуда 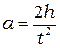 . (11.12)
. (11.12) . (11.13)
. (11.13) , так как оно много меньше ускорения свободного падения g), получают формулу для экспериментального расчета разности моментов инерции маятника при разных положениях грузов
, так как оно много меньше ускорения свободного падения g), получают формулу для экспериментального расчета разности моментов инерции маятника при разных положениях грузов . (11.14)
. (11.14)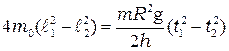 , (11.15)
, (11.15) и
и  – время прохождения грузом
– время прохождения грузом 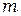 высоты h при расстояниях грузиков от оси вращения
высоты h при расстояниях грузиков от оси вращения  относительно оси вращения будет выполняться тождество (11.15), то можно говорить о том, что основной закон динамики вращательного движения выполняется.
относительно оси вращения будет выполняться тождество (11.15), то можно говорить о том, что основной закон динамики вращательного движения выполняется.


