Сила тяжести и ускорение свободного падения
Сила тяжести
Сила тяготения
где
Рис. 10.1
Центробежная сила инерции
где Центробежная сила инерции так же, как и гравитационная, зависит от широты местоположения тела. Из рис. 10.1а видно, что радиус окружности, по которой движется тело, находящееся вблизи поверхности Земли на широте j, равен
Подставив (10.4) в (10.3), находим, что центробежная сила равна нулю на полюсах (j = 90°) и максимальна на экваторе (j = 0°). Но даже на экваторе она, вследствие очень малой угловой скорости вращения Земли ( Из рис. 10.1б видно, что наличие центробежной силы инерции приводит к тому, что направление силы тяжести, совпадающее с направлением отвеса (нити, к которой прикреплен груз), или вертикальным направлением, не совпадает с направлением к центру Земли, а образует с ним угол b, зависящий от широты. Расчет показывает, что
откуда следует, что на экваторе (j = 0°) и на полюсах (j = 90°) b = 0° и отвес направлен к центру Земли. Максимального значения отклонение отвеса достигает на широте 45°, где b» 6¢ Итак, центробежная сила незначительно изменяет силу тяжести: она максимально отклоняет подвес от направления к центру Земли всего на 6¢, а ее максимальное значение составляет всего 1/291 от силы тяжести. Поэтому часто ею пренебрегают и считают, что сила тяжести равна силе тяготения (10.2), а ускорение свободного падения В настоящей работе ускорение свободного падения определяют с помощью маятников. Вариант I
|

 представляет собой геометрическую сумму гравитационной силы (силы тяготения)
представляет собой геометрическую сумму гравитационной силы (силы тяготения) 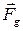 и центробежной силы инерции
и центробежной силы инерции  , учитывающей эффект суточного вращения Земли (рис. 10.1):
, учитывающей эффект суточного вращения Земли (рис. 10.1):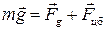 . (10.1)
. (10.1) направлена к центру Земли С, а модуль ее определяется по закону всемирного тяготения
направлена к центру Земли С, а модуль ее определяется по закону всемирного тяготения , (10.2)
, (10.2) – гравитационная постоянная,
– гравитационная постоянная,  и
и 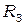 – масса и радиус Земли соответственно. Из-за сплюснутости Земли (ее экваториальный радиус на 22 км больше полярного) сила тяготения зависит от широты.
– масса и радиус Земли соответственно. Из-за сплюснутости Земли (ее экваториальный радиус на 22 км больше полярного) сила тяготения зависит от широты.
 , (10.3)
, (10.3)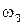 – угловая скорость вращения Земли,
– угловая скорость вращения Земли,  – радиус окружности, по которой движется тело.
– радиус окружности, по которой движется тело. сos j. (10.4)
сos j. (10.4) ,
, . Однако иногда необходимо точное знание ускорения свободного падения. Например, в геологоразведке для установления расположения тяжелых горных пород под поверхностью Земли. Есть идея использовать точное знание ускорения свободного падения в навигации.
. Однако иногда необходимо точное знание ускорения свободного падения. Например, в геологоразведке для установления расположения тяжелых горных пород под поверхностью Земли. Есть идея использовать точное знание ускорения свободного падения в навигации.


