Нормальные и касательные напряжения при поперечном изгибе
При поперечном изгибе в сечении балки помимо изгибающего момента ( На основании закона парности касательные напряжения возникают и в продольных сечениях балки. Вследствие этого при поперечном изгибе отмечаются сдвиги продольных слоев балки относительно друг друга. При поперечном изгибе гипотеза плоских сечений нарушается, поскольку поперечные сечения балки искривляются (рис. 7.9). Исследования показали: если балка является достаточно длинной, влияние искривления поперечного сечения на значения нормальных напряжений невелико, поэтому влиянием сдвигов на закон распределения нормальных напряжений при изгибе пренебрегают, формула нормальных напряжений при поперечном изгибе: Проанализируем формулу Журавского:
Поперечная сила ( Во всех точках поперечного сечения, расположенных на расстоянии y отнейтральной линии (по всей ширине сечения В самых удаленных от нейтральной оси точках поперечного сечения касательные напряжения при поперечном изгибе равны 0, поскольку в этом случае Наибольшие касательные напряжения возникают в точках поперечного сечения, расположенных на нейтральной оси. Напомним, что в этих точках нормальные напряжения равны нулю Формула Журавского позволяет определить касательные напряжения при изгибе, возникающие в точках поперечного сечении балки, находящиеся на расстоянии от нейтральной оси x.
Jx – момент инерции сечения – постоянная величина для всего сечения относительно оси Х; b– ширина сечения в рассматриваемой точке, b`const; Sx* - статический момент отсеченной части сечения площадью F
22. Формулы максимальных касательных напряжений при косом изгибе: Наибольшие касательные напряжения при косом изгибе возникают в центре тяжести поперечного сечения, которые находятся по формуле:
23. Определим ориентацию площадки, т.е. значение a = a0 , при котором напряжение sa принимает экстремальное значение. Согласно правилу определения экстремумов функций из математического анализа, возьмем производную функции sa от a и приравняем ее нулю: Согласно этому выражению, экстремальные напряжения возникают на двух взаимно перпендикулярных площадках, называемых главными, а сами напряжения - главными напряжениями. Сопоставляя выражения ta и
откуда и следует, что касательные напряжения на главных площадках всегда равны нулю. В заключение, с учетом известных тригонометрических тождеств:
и формулы определим главные напряжения, выражая из через s и t:
Полученное выражение имеет важное значение в теории прочности изгибаемых элементов, позволяющее производить расчеты их прочности, с учетом сложного напряженного состояния, присущее поперечному изгибу.
Рассмотрим расчет осей. Оси нагружены только изгибающими нагрузками и соответственно их рассчитывают на изгиб. После составления расчетной схемы и определения всех сил, действующих на ось, строят эпюру изгибающих моментов и по максимальному изгибающему моменту рассчитывают ось. Расчет осей на статическую прочность при изгибе:
\ Прочность (в физике и материаловедении) — свойство материала сопротивляться разрушению под действием внутренних напряжений, возникающих под воздействием внешних сил. Прочность подразделяют: на статическую, под действием постоянных нагрузок, Расчет на статическую прочность проводится с целью определения общего напряженно-деформированного состояния котла. По результатам напряженно-деформированного состояния проводится анализ прочности элементов конструкции и сравнение полученных напряжений с допускаемыми.
24. Деформация поперечного изгиба возникает, когда сила действует перпендикулярно оси закрепленного тела (фиг. Под влиянием силы стержень прогибается вниз. Верхние его слои сжимаются. [ 1 ] По определению деформации поперечного изгиба внешние силы перпендикулярны оси балки. Значит, компонент реакции, совпадающий по направлению с осью балки, всегда равен нулю, как единственная сила, дающая проекцию на ее направление, и на схеме нагружения Ах можно не изображать. [ 2 ] Для расчетов деталей на сочетание деформаций поперечного изгиба и кручения необходимо, как правило, составить расчетную схему конструкции и построить эпюры изгибающих и крутящих моментов, определить предположительно опасные сечения, после чего, применив одну из теорий прочности, произвести необходимые расчеты. [ 3 ] Отрезаемые параллельными ножницами полосы не подвергаются деформации поперечного изгиба или скручивания. Гильотинные ножницы применяют для отрезки более толстых листовых материалов. [ 4 ] Приведенная сила Р будет создавать на валу, на котором закреплена шестерня, деформацию поперечного изгиба, а пара сил будет скручивать вал. [ 5 ] Для вывода расчетных формул можно показать балки и других типов, нагруженные любой нагрузкой, вызывающей деформацию прямого поперечного изгиб
|

 ) возникает поперечная сила (
) возникает поперечная сила (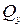 ). Поэтомув поперечном сечении при поперечном изгибе наряду с нормальными напряжениями (
). Поэтомув поперечном сечении при поперечном изгибе наряду с нормальными напряжениями ( ) возникают и касательные напряжения (
) возникают и касательные напряжения ( ).
). .
.
 являются постоянными величинами, поэтому касательные напряжения изменяются по высоте поперечного сечения по тому же закону, что и отношение статического момента отсеченной части поперечного сечения (
являются постоянными величинами, поэтому касательные напряжения изменяются по высоте поперечного сечения по тому же закону, что и отношение статического момента отсеченной части поперечного сечения ( ) к ширине поперечного сечения (
) к ширине поперечного сечения ( ), в котором они вычисляются.
), в котором они вычисляются. .
. , где
, где  – площадь поперечного сечения балки.
– площадь поперечного сечения балки. .
.
 , имеем:
, имеем: ,
,
 ,
,
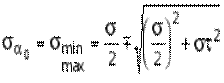 .
.




