Тема 3.13. Муфты
Назначение, классификация. Основные типы муфт, их устройство и принцип действия. Методика подбора стандартных муфт.
Литература: 1. Н.Г. Куклин, Г.С. Куклина, В.К. Житков Детали машин. 397 с. Издание шестое, переработанное и дополненное. М.: Высшая школа, 2005. 2. А.А. Эрдеди, Н.А. Эрдеди Детали машин. 288 с. Издание второе, исправленное и дополненное. М. «Высшая школа». 2001 3. М.С. Мовнин, Л.Б. Израелит, А.Г. Рубашкин Основы технической механики. 287 с. Издание 4-е, переработанное и дополненное. Санкт-Петербург. «Политехника». 2000 МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
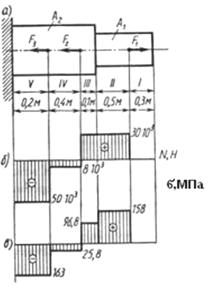
Две первые задачи каждого варианта могут быть решены после усвоения тем 2.1, 2.2, 2.4 и 2.5. Прежде чем приступить к их решению, студент должен научиться владеть методом сечений для определения внутренних силовых факторов. Эти навыки пригодятся студентам для выполнения других задач второго задания. Первая задача (задачи 61-70) требует от студента умения строить эпюры продольных сил, нормальных напряжений, определять удлинения или укорочения бруса. При работе бруса на растяжение и сжатие в его поперечных сечениях возникает продольная сила N. Продольная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме проекций на его продольную ось всех внешних сил, действующих на отсеченную часть. Для расчета на прочность и определения перемещений необходимо знать закон изменения продольных сил по его длине. Правило знаков: при растяжении продольная сила положительна, при сжатии - отрицательна. Условие прочности при растяжении и сжатии имеет вид σ = Последовательность решения задачи: 1. Разбить брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы, а для напряжений также и места изменения размеров поперечного сечения. 2. Определить по методу сечений продольную силу для каждого участка (ординаты эпюры N) и построить эпюру продольных сил N. Проведя параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получаемые значения ординат. Через концы ординат провести линии. Проставить знаки и заштриховать эпюру линиями, параллельными ординатам. 3. Для построения эпюры нормальных напряжений определяем напряжения в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянны, т.е. эпюра на данном участке изображается прямой, параллельной оси бруса. 4. Перемещение свободного конца бруса определяем как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука. Пример 8. Для данного ступенчатого бруса (рис 12, а) построить эпюру продольных сил, эпюру нормальных напряжений и определить перемещение свободного конца, если Е= 2*105 МПа = 2*1011 Па; F1= 30 кН = 30*103 Н; F2=28 кН =38*103 Н; F3=42 кН = 42*103 Н; А1=1, 9 см2 =19*10-4 м2; А2=3, 1 см2 = 3, 1*10-4 м2.
Решение: 1. Разбиваем брус на участки, как показано на рис. 12, а.
2. Определяем ординаты эпюры N на участках бруса: N1= 0; N2= F1= 30 кН; N3 = F1 = 30 кН;
Рис. 12 N4 = F1 - F2 = - 8 кН; N5= F1 - F2 - F3 = - 50 кН. σ 1 =
 = =  = 158*106 Па = 158 МПа; = 158*106 Па = 158 МПа;
σ 3 = σ 4 = σ 5 = Строим эпюру нормальных напряжений (рис. 12, в). 4. Определяем перемещение свободного конца: l= Dl1+Dl2+Dl3 +Dl4+Dl5 Dl1= Dl2= Dl3= Dl4= Dl5= - l= 0, 394+0, 0484-0, 0516-0, 161»0, 23 мм. Брус удлиняется на 0, 23 мм.
Вторая задача (задачи 71…80). К решению этой задачи следует приступить после изучения темы «Кручение». Кручением называют такой вид нагружения бруса, при котором в его поперечных сечениях возникает только один внутренний фактор- крутящий момент Мк или Мz Крутящий момент в произвольном поперечном сечении бруса равен алгебраической сумме внешних моментов, действующих на отсеченную часть: Мk= å Мi (имеется в виду, что плоскости действия всех внешних скручивающих моментов Мi перпендикулярны продольной оси бруса). Будем считать крутящий момент положительным, если для наблюдателя, смотрящего на проведенное сечение, он представляется направленным по часовой стрелке, а соответствующий внешний момент направлен против часовой стрелки (рис. 13).
 Во второй задаче необходимо выполнить проектный расчет вала круглого поперечного сечения из условий прочности и жесткости; из двух полученных значений диаметров следует выбрать наибольшее значение. Во второй задаче необходимо выполнить проектный расчет вала круглого поперечного сечения из условий прочности и жесткости; из двух полученных значений диаметров следует выбрать наибольшее значение.
Последовательность решения задачи: 1) определить внешние скручивающие моменты по формуле М= Р/w, где Р- мощность, w- угловая скорость;
2) определить уравновешивающий момент, используя уравнение равновесия å М
3) пользуясь методом сечений, построить эпюру крутящих моментов по длине вала; 4) для участка вала, в котором возникает наибольший крутящий момент, определить диаметр вала для круглого сечения из условий прочности и жесткости. Диаметр вала из условия прочности: d = Диаметр вала из условия жесткости: d = Из двух полученных диаметров выбрать большее, округленное до целого числа.
|

 ≤ [σ ], где σ, N- соответственно нормальное напряжение и продольная сила в опасном сечении (т.е. в сечении, где возникает наибольшее напряжение); А - площадь поперечного сечения; [σ ] - допускаемое напряжение. Исходя из условия прочности, можно решать три вида задач: 1) проверка прочности; 2) подбор сечения А ≥ N/ [σ ]; 3) определение допускаемой нагрузки [N] ≤ [σ ] A.
≤ [σ ], где σ, N- соответственно нормальное напряжение и продольная сила в опасном сечении (т.е. в сечении, где возникает наибольшее напряжение); А - площадь поперечного сечения; [σ ] - допускаемое напряжение. Исходя из условия прочности, можно решать три вида задач: 1) проверка прочности; 2) подбор сечения А ≥ N/ [σ ]; 3) определение допускаемой нагрузки [N] ≤ [σ ] A.
 = 0;
= 0; =
=  = 96.8*106 Па = 96, 8 МПа;
= 96.8*106 Па = 96, 8 МПа; = -
= -  =-25, 8*106 Па = - 25, 8 МПа;
=-25, 8*106 Па = - 25, 8 МПа;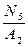 = -
= -  = -163*106 Па = - 163 МПа.
= -163*106 Па = - 163 МПа. =0
=0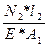 =
=  =3, 94*10-4 м =0, 394 мм;
=3, 94*10-4 м =0, 394 мм; =
=  =0, 484*10-4 м = 0, 484 мм;
=0, 484*10-4 м = 0, 484 мм;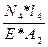 = -
= -  = - 0, 516*10-4 м = - 0, 0516мм;
= - 0, 516*10-4 м = - 0, 0516мм;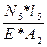 = -
= -  =- 1, 61*10-4 м = -0, 161 мм;
=- 1, 61*10-4 м = -0, 161 мм; = 0, так как при равномерном вращении вала алгебраическая сумма приложенных к нему внешних скручивающих (вращающих) моментов равна нулю;
= 0, так как при равномерном вращении вала алгебраическая сумма приложенных к нему внешних скручивающих (вращающих) моментов равна нулю;




