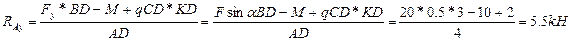Тема 1.15. Общие теоремы динамики
Импульс силы, количество движения. Теорема о количестве движения для точки. Кинетическая энергия точки. Теорема о кинетической энергии для точки. Система материальных точек. Внешние и внутренние силы системы. Основное уравнение динамики для вращательного движения твердого тела. Момент инерции тела.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
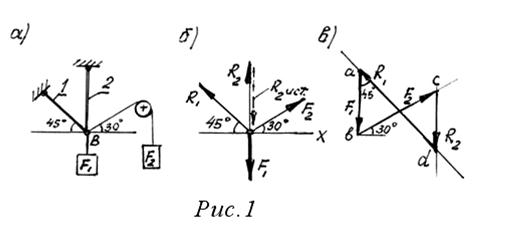
В рекомендованных учебниках [2, 3, 4], а также в руководстве [1], студенты найдут достаточное число примеров задач подобных тем, которые включены в контрольную работу. Поэтому ниже даны лишь необходимые краткие методические указания к решению задач контрольной работы. Первую задачу (задачи 1-10) следует решить после изучения тем 1.1 и 1.2. Во всех задачах рассматривается равновесие плоской системы сходящихся сил и требуется определить реакции двух шарнирно соединенных между собой стержней, удерживающих два груза. Таким образом, к шарниру В в каждой задаче приложены четыре силы, из которых две неизвестны. Для задач этого типа универсальным является аналитический метод решения. Последовательность решения задачи: 1) выбрать тело (точку), равновесие которого следует рассматривать; 2) освободить тело (шарнир В) от связей и изобразить действующие на него активные силы и реакции отброшенных связей. Причем реакции стержней следует направить от шарнира В, так как принято считать предположительно стержни растянутыми; 3) выбрать систему координат, совместив ее начало с точкой В, и составить уравнения равновесия, используя условия равновесия системы сходящихся сил на плоскости Σ Хi=0; Σ Yi=0; 4) определить реакции стержней из решения указанной системы уравнений; 5) проверить правильность полученных результатов по уравнениям, которые не использовались при решении задачи, либо решить задачу графически. Пример 1. Определить реакции стержней, удерживающих грузы F1=70кН и F 2=100 кН (рис. 1, а). Массой стержней пренебречь. 1. Рассматриваем равновесие шарнира В (рис. 1, а). 2. Освобождаем шарнир В от связей и изображаем действующие на него активные силы и реакции связей (рис. 1, а). 3. Выбираем систему координат и составляем уравнения равновесия для системы сил, действующих на шарнир В. Σ Х = - R1 cos 450 + F2 cos 300 = 0. (1) Σ Y = R1 sin 450 + R2 + F2 sin 300 – F1 = 0. (2)
4. Определяем реакции стержней R1 и R2, решая уравнения (1), (2). Из уравнения (1)
Подставляем найденное значение R1 в уравнение (2) и получаем: R2 = F1 – F2 sin 300 – R1 sin 450 = 70-100*0.5-122.6*0.707 = - 66.6 кН. Знак минус перед значением R2 указывает на то, что первоначально выбранное направление реакции неверное – следует направить реакцию R2 в противоположную сторону, т.е. к шарниру В (на рис. 1, б истинное направление реакции R2 показано штриховым вектором). 5. Проверяем правильность полученных результатов, решая задачу графически (рис. 1, в). Полученная система сил (рис. 1, б) находится в равновесии, следовательно, силовой многоугольник, построенный для этой системы сил, должен быть замкнутым. Строим силовой многоугольник в следующем порядке (рис. 1, в): в выбранном масштабе (например, μ сил= 2 кН/мм) откладываем заданную силу F1 ( Графическое решение подтверждает правильность первого решения. Вторую задачу (задача 11-20) следует решать после изучения тем 1.3 и 1.4. Во всех задачах требуется определить реакции опор балок. Студентам необходимо приобрести навыки определения реакций опор, так как с этого начинается решение многих задач по сопротивлению материалов и деталям машин. Последовательность решения задачи: 1) изобразить балку вместе с нагрузками; 2) выбрать расположение координатных осей, совместив ось x с балкой, а ось y направив перпендикулярно оси x; 3) произвести необходимые преобразования заданных активных сил: силу, наклоненную к оси балки под углом α, заменить двумя взаимно перпендикулярными составляющими, а равномерно распределенную по закону прямоугольника нагрузку – ее равнодействующей, приложенной в середине участка распределения нагрузки; 4) освободить балку от опор, заменив их действие реакциями опор, направленными вдоль выбранных осей координат; 5) составить уравнения равновесия статики для произвольной плоской системы сил, таким образом и в такой последовательности, чтобы решением каждого из этих уравнений было определение одной из неизвестных реакций опор; 6) проверить правильность найденных опорных реакций по уравнению, которое не было использовано для решения задачи.
Пример 2. Определить реакции опор балки (рис. 2, а).
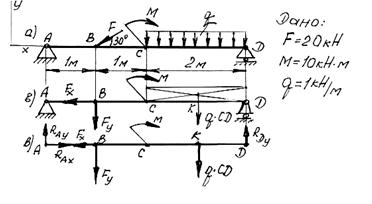 1. Изобразим балку с действующими на нее нагрузками (рис. 2, а). 1. Изобразим балку с действующими на нее нагрузками (рис. 2, а).
2. Изобразим оси координат x и y.
Fy = F sin α. Равнодействующая qCD равномерно распределенной нагрузки, приложенная в точке пересечения диагоналей прямоугольника (рис. 2, б), переносится по линии своего действия в середину участка CD, в точку K. 4. Освобождаем балку от опор, заменив их опорными реакциями (рис. 2, в). 5. Составляем управления равновесия статики и определяем неизвестные реакции опор. а) Из уравнения суммы моментов всех действующих на балку сил, составленного относительно одной из точек опор, сразу определяем одну из неизвестных вертикальных реакций: Σ MA = Fy*AB + M + qCD*AK - RD*AD = 0;
б) Определяем другую вертикальную реакцию: Σ MD = RAv*AD - F*BD + M - qCD*KD = 0;
в) Определяем горизонтальную реакцию: Σ X = RAx – Fx = 0; RAx = Fx = F cos α = 20*0.866 = 17.3 kH 5. Проверяем правильность найденных результатов: 6. Σ Y = RAy – Fy – qCD + RDy = 5.5 – 10 – 2 + 6.5 = 0. Условие равновесия Σ Y=0 выполняется, следовательно, реакции опор найдены верно.
|

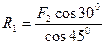 =
= 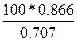 =122.6 кН
=122.6 кН =
=  ) затем из точки b под углом 300 к горизонту откладываем силу F2 (
) затем из точки b под углом 300 к горизонту откладываем силу F2 (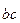 =
=  ), далее из точек a и c проводим прямые, параллельные положениям стержней 1 и 2. Эти прямые пересекаются в точке d и в результате построения образуется замкнутый многоугольник abcd, в котором сторона
), далее из точек a и c проводим прямые, параллельные положениям стержней 1 и 2. Эти прямые пересекаются в точке d и в результате построения образуется замкнутый многоугольник abcd, в котором сторона  =
= 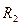 , а сторона
, а сторона  =
= 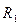 . Измерив длины этих сторон (в мм) и умножив на масштаб построения μ сил, получаем значения реакций стержней: R2 = cd* μ спл = 33*2 = 66 кН и R1 = daμ сил = 61*2=122 кН.
. Измерив длины этих сторон (в мм) и умножив на масштаб построения μ сил, получаем значения реакций стержней: R2 = cd* μ спл = 33*2 = 66 кН и R1 = daμ сил = 61*2=122 кН.