ВВОДНОЕ ЗАНЯТИЕ
МЕХАНИКА
Учебно-методическое пособие к лабораторным занятиям ПРАВИЛА ТЕХНИКИ БЕЗОПАСНОСТИ
К лабораторным занятиям допускаются студенты, прошедшие инструктаж по технике безопасности, усвоившие безопасные методы работы и расписавшиеся в журнале по технике безопасности. При проведении работ студенты обязаны соблюдать следующие меры безопасности: - не работать на неисправном оборудовании; - не применять сломанных электрических вилок, розеток, оголенных проводов для подключения приборов к сети; - не касаться токоведущих элементов; - надежно закреплять подвижные грузы; - не оставлять без присмотра включенную лабораторную установку; - после проведения измерений отключить приборы от сети; - не загромождать проходы стульями, сумками; - по окончании работы привести рабочее место в порядок; - использовать измерительные приборы и инструменты по прямому назначению.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТ
Изучить теоретический материал по данному пособию, учебнику, конспекту лекций. Ответить преподавателю на контрольные вопросы по теории работы, по выполнению эксперимента. Получить допуск к проведению лабораторной работы. Провести эксперимент в соответствии с рекомендациями по выполнению работы. Внести результаты измерений в свой формуляр отчета. Представить результаты измерений для проверки корректности измерений преподавателю. Произвести расчеты, оценить погрешности измерений. Построить при необходимости графики, проанализировать результаты, сделать выводы. Сдать оформленный отчет преподавателю.
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Измерением называют операцию, посредством которой определяется отношение измеряемой величины к другой однородной величине, принятой за единицу измерения. Обработка результатов измерений заключается в нахождении так называемого доверительного интервала значений измеряемой величины, внутри которого находится истинное значение с заданной вероятностью. Произвести измерения абсолютно точно в принципе невозможно, всякое измерение содержит погрешность. Абсолютной погрешностью называют разность между измеренным значением и истинным, которое обычно неизвестно: Δ Х = (X изм – X ист). Погрешности измерений могут быть обусловлены различными факторами. Часть суммарной погрешности, вызванная действием большого числа неконтролируемых факторов, которые непредсказуемо влияют на результаты измерений и приводят к тому, что результаты многократных измерений случайным образом изменяются, называется случайной погрешностью, δ Х. Случайные погрешности приближенно оцениваются методами математической статистики по результатам многократных измерений. Другая часть суммарной погрешности называется систематической погрешностью, θ Х. Она обусловлена действием некоторых постоянных факторов, которые можно учесть и исключить, например: заменить грубый прибор более точным, усовершенствовать методику измерений, учесть влияние незначительных факторов. Трудность заключается в обнаружении факторов влияния. Существует еще один вид погрешности, обусловленный невнимательностью экспериментатора − неверный отсчет по шкале или неверная запись результата, – это грубая погрешность, или промах. Он обнаруживается, если одно из измерений сильно отличается от других. Поэтому следует производить не менее трех измерений. Измерение с промахом либо исключается, либо исправляется, если исправление достоверно. Суммарная погрешность определяется как результирующая обоих видов погрешности:
Погрешности прямых измерений
Прямые измерения – это измерения, при которых результат определяется по шкале прибора, инструмента. Пусть проведены многократные измерения n раз при одинаковых условиях. Если все результаты одинаковы, что бывает при использовании грубого прибора, то за оценку истинного значения принимают результат любого измерения. Погрешность измерения обусловлена только систематической погрешностью прибора. Если результаты различаются, то в связи со случайностью погрешности по знаку и величине за оценку истинного значения принимают среднее арифметическое результатов отдельных измерений
Только при бесконечно большом числе измерений и при отсутствии систематической погрешности среднее значение совпадет с истинным значением. На практике число измерений конечно, и поэтому среднее отличается от истинного значения измеряемой величины. Теория погрешностей позволяет только оценить доверительный интервал, то есть интервал значений около среднего, внутри которого находится истинное значение при заданной доверительной вероятности Р. Здесь доверительная вероятность – это вероятность попадания истинного значения внутрь доверительного интервала. Погрешность измерения Δ Х принимают равной половине доверительного интервала, то есть истинное значение находится внутри доверительного интервала от < X > − Δ X до < X> + Δ X с вероятностью Р. Пусть проведены многократные измерения. Разделим числовую ось Х на большое количество небольших отрезков, на них построим прямоугольники, высота которых равна доле результатов измерений, попадающих в данный отрезок (рис.1). Если бы число измерений было бесконечно велико, то полученная ступенчатая фигура приобрела бы симметричную форму, а ее огибающая была бы плавной колоколообразной кривой линией. Описывает ее функция, полученная Гауссом при следующих предположениях: отклонения одинаковой величины разного знака равновероятны, большие отклонения от среднего встречаются реже, чем малые. Функция Гаусса имеет вид
С учетом указанных факторов случайную погрешность среднего арифметического оценивают по формуле
Чем больше число измерений n, тем ближе среднее значение к истинному значению, тем меньше случайная погрешность. В этом и состоит необходимость многократных измерений. Однако разумное число опытов должно быть таким, чтобы случайная погрешность была сравнима или чуть меньше систематической погрешности.
Таблица коэффициентов Стьюдента tp
Систематическую погрешность θ X измерительных приборов при прямых измерениях оценивают либо как половину цены деления шкалы инструмента, либо по классу точности прибора. Класс точности – это выраженное в процентах отношение систематической погрешности к пределу измерения. Он имеет значения от 0, 05 % до 4 %. Систематическую погрешность прибора определеляют по формуле
Систематическую погрешность в других случаях оценивает сам экспериментатор, исходя из здравого смысла. Суммарную погрешность Δ X измерений определяют по формуле Результат обработки результатов измерений всегда записывают в виде трех чисел: среднего арифметического, суммарной погрешности и доверительной вероятности: X = < X> ±D X, Р =….%. Это следует понимать так: истинное значение находится в доверительном интервале от < X> − D X до < X> + D X с доверительной вероятностью, например Р = 90 %. Погрешности косвенных измерений При косвенных измерениях значение измеряемой величины определяется по функциональной зависимости через аргументы, величины которых являются результатами прямых измерений. Среднее значение результата косвенных измерений определяют, подставляя в функцию средние значения аргументов, полученных как результаты прямых измерений:
< Z> = f (< X>, < Y> …), (4)
либо функцию Z рассчитывают столько раз, сколько раз измерены аргументы X, Y… и затем находят среднее арифметическое рассчитанных результатов Zi по формуле (1). Оценку случайной погрешности при косвенных измерениях производят одним из четырех способов. Способ 1. По формуле, полученной на основании аналогии между погрешностью и дифференциалом функции, как малых приращений функции. При этом учитывают, что погрешности измерений величин, входящих в формулу, никогда не компенсируют друг друга, в отличие от дифференциалов, и складываются геометрически
При этом погрешности измерения аргументов должны быть определены с одинаковой доверительной вероятностью. По этой же формуле оценивается систематическая погрешность косвенного измерения θ Z через систематические погрешности аргументов функции. В данном пособии расчетные формулы выведены. Способ 2. Величину Z рассчитывают по результатам измерений аргументов функции столько раз, сколько проведено прямых измерений. Совокупность результатов обрабатывают как при прямых измерениях. То есть случайную погрешность оценивают по формуле (2). Способ 3. Графический метод. Пусть измеряемая величина теоретически является линейной функцией Z = Z 0 + K X. В этом случае около экспериментальных точек на графике проводят прямую линию. Ордината точки пересечения прямой линии с осью Z дает среднее значение величины < Z 0 >;. Для оценки случайной погрешности δ Z 0 проводят параллельно экспериментальной линии две прямых так, чтобы все точки, кроме промахов, оказались между ними (рис. 2, пунктирные линии). Тогда половину расстояния между ними вдоль оси ординат можно трактовать как 2÷ 3 среднеквадратичных погрешности σ Z 0/2 = (2 ÷ 3) S.
Для определения среднего значения углового коэффициента < K> построим на экспериментальной линии как на гипотенузе прямоугольный треугольник. Среднее значение найдем как отношение катетов треугольника:
Для оценки случайной погрешности измерения углового коэффициента проведем на графике две диагонали параллелограмма области существования экспериментальных точек. Их угловые коэффициенты определим по координатам вершин параллелограмма как отношение катетов:
Здесь σ Z – расстояние по ординате между вспомогательными (пунктирными на рис.2) линиями. Способ 4. В научных исследованиях применяют для проведения средней прямой и для оценки случайной погрешности метод наименьших квадратов. Но расчеты достаточно трудоемкие. Поэтому в данном пособии отдается предпочтение простому графическому методу, дающему почти тот же результат. Суммарную погрешность измерения определяют по формуле
ПРАВИЛА ПОСТРОЕНИЯ ГРАФИКОВ График – это геометрическое изображение функциональной зависимости. Это самое наглядное представление результатов эксперимента. График строится на миллиметровой или клетчатой бумаге. Вычерчиваются координатные оси. Для функции используется ось ординат, для аргумента – ось абсцисс. На осях наносят масштаб так, чтобы расстояние между делениями (1 см) составляло 1, 2, 5 единиц измеряемой величины. У оси указывают измеряемую величину, размерность и ее порядок (10к). Масштаб выбирают так, чтобы экспериментальная линия заняла всю площадь графика. Поэтому наибольшее значение измеряемой величины должно быть близко к концу координатной оси. Вдоль оси указывают около пяти значений координат через равные промежутки. Если результаты находятся в диапазоне, далеком от нуля, то рекомендуется в начале координат помещать самое малое округленное значение (рис. 3). Размер графика не менее половины страницы. Точки следует наносить тщательно, обводя их каким-либо значком (○, ●, □, +). Около точек, но не через них, проводится экспериментальная кривая линия. При этом следует руководствоваться правилами: линия должна быть гладкая, чем больше изгибов имеет линия, тем она менее вероятна; число точек выше и ниже линии должно быть примерно одинаковым; сумма квадратов отклонений точек от экспериментальной линии должна быть минимальна, поэтому не должно быть больших отклонений, лучше 2 – 3 маленьких.
Типичными ошибками при построении графиков являются: нанесение экспериментальных данных на оси координат, вместо равномерного масштаба; проведение линий для построения экспериментальных точек; малый размер графика (менее половины страницы).
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Объясните причину оценки неизвестного истинного значения средним арифметическим результатов измерений. 2. Чем обусловлены случайная и систематическая погрешности прямых измерений? Что такое промах, как его обнаружить и как с ним поступать? 3. Дайте определение доверительного интервала, доверительной вероятности. 4. Как зависит случайная погрешность среднего арифметического многократных измерений от среднеквадратичной погрешности отдельного измерения, от числа измерений, от доверительной вероятности? 5. Прокомментируйте формулу для оценки случайной погрешности прямых измерений. Как определяется коэффициент Стьюдента? 6. Как оценивается систематическая погрешность прямых измерений для классифицированного прибора, для линейки и для цифрового прибора? 7. Как оценивается суммарная погрешность результата измерений? Как записывается результат измерений? 8. Прокомментируйте формулу, по которой оцениваются случайная и систематическая погрешности косвенных измерений, полученную на основании аналогии погрешности с дифференциалом функции. 9. Объясните способ оценки случайной погрешности косвенных измерений сведением к формуле погрешности для прямых измерений. 10.Выведите расчетную формулу графического определения среднего значения и случайной погрешности углового коэффициента. 11.Объясните правила выбора масштаба координатных осей графика. 12.Перечислите правила проведения на графике линии относительно экспериментальных точек. 13. Перечислите основные ошибки при построении графика.
Работа 1
|

 . Точность измерений характеризуют относительной погрешностью
. Точность измерений характеризуют относительной погрешностью  .
. . (1)
. (1) . Здесь σ – среднеквадратичное отклонение результатов измерений относительно истинного значения при бесконечно большом числе измерений (так называемый стандарт). Оно характеризует точность отдельных измерений: чем оно меньше, тем выше точность эксперимента. В интервал ± σ попадает 68 % результатов измерений, в интервал ±2 σ – 95, 3 % и в интервал ±3 σ – 99, 7%. Так как число измерений всегда конечно, то среднеквадратичное отклонение результатов отдельных измерений определяют относительно среднего значения < X> по формуле
. Здесь σ – среднеквадратичное отклонение результатов измерений относительно истинного значения при бесконечно большом числе измерений (так называемый стандарт). Оно характеризует точность отдельных измерений: чем оно меньше, тем выше точность эксперимента. В интервал ± σ попадает 68 % результатов измерений, в интервал ±2 σ – 95, 3 % и в интервал ±3 σ – 99, 7%. Так как число измерений всегда конечно, то среднеквадратичное отклонение результатов отдельных измерений определяют относительно среднего значения < X> по формуле  . Здесь под корнем стоит сумма квадратов разностей между результатами всех измерений и их средним значением.
. Здесь под корнем стоит сумма квадратов разностей между результатами всех измерений и их средним значением.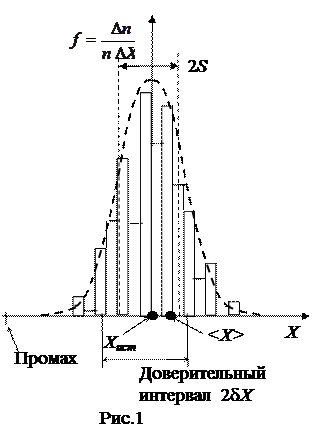 Среднее значение конечно ближе к истинному значению, чем результаты отдельных измерений, но оно также является случайной величиной. Применяя к нему распределение Гаусса (как будто имеем много средних значений), получим, что среднеквадратичное отклонение среднего значения равно
Среднее значение конечно ближе к истинному значению, чем результаты отдельных измерений, но оно также является случайной величиной. Применяя к нему распределение Гаусса (как будто имеем много средних значений), получим, что среднеквадратичное отклонение среднего значения равно  . Чем большую доверительную вероятность необходимо гарантировать, тем доверительный интервал и случайная погрешность должны быть больше. Это учитывается умножением Sср на коэффициент Стьюдента tр.
. Чем большую доверительную вероятность необходимо гарантировать, тем доверительный интервал и случайная погрешность должны быть больше. Это учитывается умножением Sср на коэффициент Стьюдента tр. 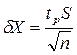 или
или . (2)
. (2) . (3)
. (3) . Если одна из погрешностей меньше другой более чем в 3 раза, меньшей пренебрегают. Так как при числе опытов менее 10 уже первая цифра погрешности не достоверна, то расчеты погрешности следует производить приближенно с точностью до одной значащей цифры, может быть, даже устно.
. Если одна из погрешностей меньше другой более чем в 3 раза, меньшей пренебрегают. Так как при числе опытов менее 10 уже первая цифра погрешности не достоверна, то расчеты погрешности следует производить приближенно с точностью до одной значащей цифры, может быть, даже устно. . (5)
. (5) Случайная погрешность, как известно, оценивается по формуле
Случайная погрешность, как известно, оценивается по формуле  . Коэффициент Стьюдента при числе измерений менее десяти имеет значение между 2 и 3,
. Коэффициент Стьюдента при числе измерений менее десяти имеет значение между 2 и 3,  . Подставив
. Подставив  и сокращая на коэффициент Стьюдента, получим
и сокращая на коэффициент Стьюдента, получим . (6)
. (6) . (7)
. (7) и
и 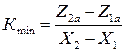 . Примем половину разности угловых коэффициентов за (2÷ 3) среднеквадратичных погрешности углового коэффициента:
. Примем половину разности угловых коэффициентов за (2÷ 3) среднеквадратичных погрешности углового коэффициента: 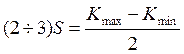 . Тогда случайную погрешность углового коэффициента
. Тогда случайную погрешность углового коэффициента 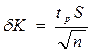 можно, сокращая на значение коэффициента Стьюдента tр =(2÷ 3), оценить по формуле
можно, сокращая на значение коэффициента Стьюдента tр =(2÷ 3), оценить по формуле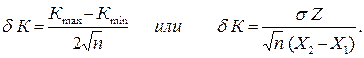 (8)
(8)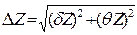 . Так как при числе измерений менее десяти уже первая значащая цифра погрешности не является достоверной, расчеты можно произвести устно с точностью до одного знака. Тем более не следует списывать с индикатора калькулятора все восемь цифр, спишите округленное первое. Если одна из погрешностей меньше другой в три и более раз, то меньшей пренебрегают. Результат следует записать в виде трех чисел: Z = < Z> ±Δ Z, Р =…... Среднее арифметическое округляют так, чтобы разряд последней цифры совпадал с разрядом погрешности: например, J = (3, 42±0, 06)·10-3 кг·м2, Р= 90 %.
. Так как при числе измерений менее десяти уже первая значащая цифра погрешности не является достоверной, расчеты можно произвести устно с точностью до одного знака. Тем более не следует списывать с индикатора калькулятора все восемь цифр, спишите округленное первое. Если одна из погрешностей меньше другой в три и более раз, то меньшей пренебрегают. Результат следует записать в виде трех чисел: Z = < Z> ±Δ Z, Р =…... Среднее арифметическое округляют так, чтобы разряд последней цифры совпадал с разрядом погрешности: например, J = (3, 42±0, 06)·10-3 кг·м2, Р= 90 %.
 Если известна теоретическая зависимость, то около точек проводится линия теоретической зависимости. Отклонения точек от линии обусловлены случайными погрешностями измерений. При возможности свести теоретическую зависимость к линейной проводят операцию линеаризации, так как прямую линию можно провести наиболее надежно. Например, для функции
Если известна теоретическая зависимость, то около точек проводится линия теоретической зависимости. Отклонения точек от линии обусловлены случайными погрешностями измерений. При возможности свести теоретическую зависимость к линейной проводят операцию линеаризации, так как прямую линию можно провести наиболее надежно. Например, для функции  график − кривая линия, экспонента, но если функцию прологарифмировать
график − кривая линия, экспонента, но если функцию прологарифмировать  , то получаем уравнение прямой линии, которую построить гораздо проще (рис. 3).
, то получаем уравнение прямой линии, которую построить гораздо проще (рис. 3).


