КРУТИЛЬНЫМ МАЯТНИКОМ
Цель работы: определить скорость пули с помощью крутильно-баллистического маятника, познакомиться с применением закона сохранения момента импульса. Оборудование: крутильно-баллистический маятник с мишенью, пружинный пистолет, пуля, секундомер.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Скорость пули можно определить с помощью крутильно-баллистического маятника. Это обусловлено тем, что после удара маятник поворачивается на угол, пропорциональный скорости пули. Крутильно-баллистический маятник – это массивное по сравнению с пулей тело произвольной формы, подвешенное на упругих нитях. Пусть горизонтально летящая пуля на расстоянии r от оси попадает в мишень маятника и застревает в ней (рис. 1). После удара маятник и пуля поворачиваются совместно, и это является признаком неупругого удара. Так как процесс удара является кратковременным, то за время удара маятник не успевает повернуться и силы упругости незакрученных нитей подвеса отсутствуют. Действуют только сравнительно большие внутренние силы удара. Значит, система тел пуля – маятник на время удара является замкнутой. Поэтому выполняется закон сохранения момента импульса: в замкнутой системе тел сумма моментов импульсов тел постоянна или сумма моментов импульсов тел до взаимодействия тел равна сумме моментов импульсов тел после взаимодействия: Моментом импульса твердого тела относительно оси называется аксиальный вектор, то есть вектор, направленный по оси вращения, равный произведению момента инерции тела на вектор угловой скорости:
mV r = (mr2 + J) w 0. (1)
Если пренебречь добавкой момента инерции пули mr 2 к моменту инерции маятника, то уравнение закона сохранения момента импульса будет иметь более простой вид: mVr = Jw 0. Отсюда получим формулу для скорости пули
Угловую скорость w 0 маятника и момент инерции J можно определить из уравненияколебаний. Если маятник вывести от положения равновесия и отпустить, то он под действием момента упругих сил подвеса будет поворачиваться к положению равновесия, но по инерции пройдет его и отклонится в противоположную сторону. Затем процесс повторится, то есть возникнут вращательные колебания. Уравнение основного закона динамики вращательного движения имеет вид: произведение момента инерции маятника на угловое ускорение
Решением уравнения является функция, превращающая его в тождество. Это могут быть функции косинуса или синуса:
где a 0– амплитуда колебаний, то есть наибольший угол отклонения маятника; Т 0 – период колебаний, то есть время одного колебания. Если подставить функцию (4) в уравнение (3), то оно обратится в тождество при условии, если период колебаний маятника будет равен
Из этой формулы момент инерции определить пока невозможно, так как неизвестен коэффициент упругости подвеса k. Чтобы его исключить, наденем на штыри рамки два груза с массой mгр на расстоянии l от оси. Момент инерции маятника изменяется на величину, 2 mгр l 2. Период колебаний маятника тоже изменится и станет равным
Решая уравнения (6) и (5), исключив коэффициент k, получим формулу для момента инерции
Получим формулу для расчета угловой скорости маятника. Угловая скорость, по определению, равна первой производной от угла поворота по времени. Дифференцируя уравнение (4), получим
Крутильный маятник представляет собой рамку, подвешенную к кронштейну на стальных струнах. На рамке установлена штанга с мишенью и противовесом. Выстрел пулей производится с помощью пружинного пистолета. Угол отклонения штанги маятника определяется по шкале по положению флажка на штанге. Период колебаний определяется с помощью секундомера, управляемого фотоэлементом.
ВЫПОЛНЕНИЕ РАБОТЫ
1. Убедиться, что линия полета пули проходит через мишень, рамка может колебаться, не задевая фотоэлемент; в положении равновесия флажок рамки находится против нуля шкалы. При необходимости отрегулировать. Снять добавочные грузы. 2. Взвести пружинный пистолет с пулей. Произвести выстрел в мишень. Измерить угол первого отклонения маятника по шкале a 0. Измерить расстояние от оси до точки удара пули r. Опыт произвести не менее пяти раз. Результаты записать в табл.1. Таблица 1
3. Определить массу пули, массу грузов, измерить расстояние от оси до середины грузов l. Результаты записать в табл. 2. Включить установку в сеть 220 В. 4. Измерить период колебаний маятника без грузов Т 0. Для этого нажать кнопку «Сеть» (на задней панели секундомера), отвести рамку маятника на небольшой угол к электромагниту, магнит притянет рамку. Нажать кнопку «Пуск», магнит отпустит рамку. Начнется счет времени и числа колебаний. Чтобы измерить время десяти колебаний t, следует после совершения девятого колебания нажать кнопку «Стоп» секундомера. Период равен T 0 =t/ 10. Записать в табл. 2. 5. Измерить период колебаний Т 1 рамки с грузами. Для этого надеть на рамку добавочные грузы. Нажать кнопку «Сброс» для обнуления индикаторов и включения магнита. Отвести рамку к магниту, нажать «Пуск», измерить время десяти колебаний. Результат записать в табл. 2. Выключить установку. Таблица 2
6. Произвести расчеты в системе СИ. Определить момент инерции маятника по формуле (7). Определить среднее значения угла поворота < a 0 >. Рассчитать среднее значение амплитуды угловой скорости < w 0 > по формуле (8) по среднему значению угла < α 0 >. Результаты записать в табл. 1 и 2. Определить среднее значение скорости < V> по формуле (2). 7. Оценить случайную погрешность измерений скорости пули, полагая, что основной вклад вносит случайная погрешность измерения угла поворота, по формуле
8. Записать результат работы в виде V = < V> ± d V, P = 0, 9. Сделать выводы. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дайте определение крутильного маятника. Выведите и объясните формулу для периода колебаний маятника. 2. Дайте определение момента импульса материальной точки, твердого тела. Как определить направление момента импульса тела? 3. Сформулируйте закон сохранения момента импульса. Почему его можно применить для процесса удара пули о мишень маятника? 4. Запишите закон сохранения момента импульса для удара пули о мишень маятника. 5. Сделайте вывод формулы для расчета амплитуды угловой скорости маятника. 6. Объясните метод определения момента инерции маятника с помощью добавочных грузов.
Работа 6
|

 .
. . Моментом импульса материальной точки называют вектор, равный векторному произведению радиус-вектора точки r на вектор импульса
. Моментом импульса материальной точки называют вектор, равный векторному произведению радиус-вектора точки r на вектор импульса  . Направление вектора момента импульса, как и угловой скорости, определяется правилом буравчика. Если вращать буравчик вместе с телом, то вектор угловой скорости совпадает по направлению с поступательным движением буравчика.
. Направление вектора момента импульса, как и угловой скорости, определяется правилом буравчика. Если вращать буравчик вместе с телом, то вектор угловой скорости совпадает по направлению с поступательным движением буравчика.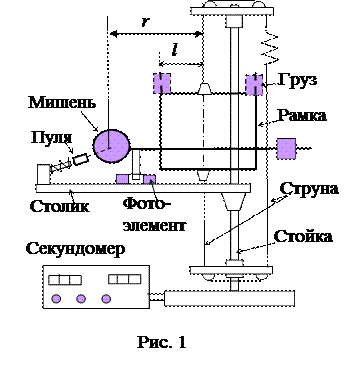 Пулю, размер которой много меньше расстояния от линии полета до оси вращения маятника r, можно считать материальной точкой. По закону сохранения момента импульса момент импульса пули до удара равен моменту импульса маятника с застрявшей пулей после удара. В проекции на ось вращения уравнение будет иметь вид
Пулю, размер которой много меньше расстояния от линии полета до оси вращения маятника r, можно считать материальной точкой. По закону сохранения момента импульса момент импульса пули до удара равен моменту импульса маятника с застрявшей пулей после удара. В проекции на ось вращения уравнение будет иметь вид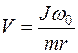 . (2)
. (2)
 равно моменту упругих сил подвеса М = − ka.:
равно моменту упругих сил подвеса М = − ka.: . (3)
. (3) , (4)
, (4) . (5)
. (5)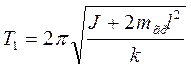 . (6)
. (6) . (7)
. (7)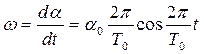 . Отсюда угловая скорость маятника сразу после удара, при t = 0, может быть рассчитана по формуле
. Отсюда угловая скорость маятника сразу после удара, при t = 0, может быть рассчитана по формуле . (8)
. (8) , где
, где 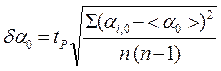 . (9)
. (9)


