ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ. Плоскимявляется движение, при котором траектории точек тела лежат в параллельных плоскостях
Плоскимявляется движение, при котором траектории точек тела лежат в параллельных плоскостях. Плоское движение можно представить двумя способами.
Возможно другое представление плоского движения. Пусть скорость точки О – центра масс тела равна Примером плоского движения является качение колеса по плоскости. Если проскальзывания нет, то мгновенная ось вращения совпадает с линией касания колеса с плоскостью, перемещаясь по плоскости. Соответственно двум способам представления уравнениями динамики могут быть: либо основной закон динамики вращательного движения относительно мгновенной оси
либо система уравнений второго закона Ньютона для поступательного движения центра масс и основного закона динамики вращательного движения тела относительно оси, проходящей через центр масс
В уравнениях J 0 и Jс – моменты инерции тела относительно выбранных осей вращения О или С. Момент инерции является мерой инертности тела при вращательном движении и по определению равен сумме произведений масс mi (dm)частиц тела на квадраты их расстояний r до оси вращения: Соотношение между моментами инерции J 0 и Jc можно установить, если подставить в уравнение (1) момент силы F относительно мгновенной оси С
Это уравнение теоремы Штейнера: момент инерции тела относительно произвольной оси С равен сумме момента инерции относительно оси, проходящей через центр масс О, параллельной данной оси С и произведению массы тела на квадрат расстояния между осями. Для экспериментального определения момента инерции тел вращения рассмотрим скатывание с наклонной плоскости, расположенной под углом a к горизонту (рис.2). Представим скатывание тела как вращение вокруг мгновенной оси С под действием силы тяжести.Плечо силы тяжести относительно оси С равно
Подставим в уравнение динамики вращательного движения относительно мгновенной оси С (1) формулы момента силы тяжести, момента инерции
Для тел вращения (кольцо, диск, шар) момент инерции можно рассчитать теоретически по определяющей формуле, взяв интеграл Более важно определить не само значение момента инерции, а отношение
Так как все силы постоянны, то движение тела равноускоренное. Значит, ускорение а можно определить по времени скатывания телом некоторого расстояния S по уравнению кинематики
Как видно, средняя скорость скатывания тела до каждого фотоэлемента,  , линейно зависит от времени. Поэтому, если построить график линейной зависимости < V > (t), то по нему можно определить ускорение как удвоенное значение углового коэффициента линии (рис.4) , линейно зависит от времени. Поэтому, если построить график линейной зависимости < V > (t), то по нему можно определить ускорение как удвоенное значение углового коэффициента линии (рис.4)
ВЫПОЛНЕНИЕ РАБОТЫ
1. Включить блок питания в сеть 220 В. Установить некоторый угол наклона желоба. Расположить одно из тел (кольцо, диск, шар) около верхнего упора. Отпустить. Повторить опыт несколько раз и убедиться в повторяемости показаний. Записать в табл. 1 время скатывания до фотоэлементов в одном из опытов.
Таблица 1 Выключить установку. 2. Произвести расчеты. Определить среднее значение скорости скатывания до каждого фотоэлемента 3. Построить график зависимости средней скорости от времени движения до каждого фотоэлемента. Размер графика не менее половины страницы. На осях координат указать равномерный масштаб. Около экспериментальных точек провести прямую линию. Таблица 2
4. Рассчитать по координатам крайних точек А и В на экспериментальной линии среднее ускорение по формуле (7). Определить среднее экспериментальное значение параметра К экс по формуле (6). Записать в табл. 2 параметры и результаты расчета. 5. Сравнить экспериментальное значение параметра
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дайте определение плоского движения. Каким образом можно представить плоское движение? Дайте определение мгновенной оси. Каким образом можно установить её положение? 2. Запишите уравнения динамики для плоского движения в двух способах представления движения. 3. Дайте определение момента силы, плеча силы. Запишите формулу для момента силы тяжести тела на наклонной плоскости. 4. Дайте определение момента инерции. Выведите и сформулируйте теорему Штейнера. 5. Выведите расчётную формулу для определения момента инерции тел, скатывающихся с наклонной плоскости. 6. Запишите формулы момента инерции для кольца, диска, шара относительно оси симметрии. Работа 9
|

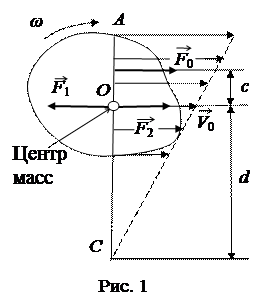 Пусть к телу в некоторой точке приложена сила F 0 (рис. 1). Приложим к особой точке тела, называемой центром масс, две равные и противоположные силы F 1 и F 2, параллельные и равные силе F 0. Под действием силы F 2 тело совершает поступательное движение, а пара сил F 0 и F 1создает момент сил M 0 =F 0 c, под действием которого тело вращается. Итак, тело одновременно движется поступательно со скоростью центра масс и вращается вокруг оси, проходящей через центр масс.
Пусть к телу в некоторой точке приложена сила F 0 (рис. 1). Приложим к особой точке тела, называемой центром масс, две равные и противоположные силы F 1 и F 2, параллельные и равные силе F 0. Под действием силы F 2 тело совершает поступательное движение, а пара сил F 0 и F 1создает момент сил M 0 =F 0 c, под действием которого тело вращается. Итак, тело одновременно движется поступательно со скоростью центра масс и вращается вокруг оси, проходящей через центр масс.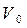 (рис.1). Проведём в плоскости движения перпендикуляр АОС к вектору скорости V 0. Так как тело твёрдое, то огибающая векторов является прямой линией. Она и перпендикуляр пересекутся в некоторой точке С, скорость этой точки равна нулю. Через неё проходит так называемая мгновенная ось, относительно которой тело совершает только вращение. Положение мгновенной оси со временем меняется.
(рис.1). Проведём в плоскости движения перпендикуляр АОС к вектору скорости V 0. Так как тело твёрдое, то огибающая векторов является прямой линией. Она и перпендикуляр пересекутся в некоторой точке С, скорость этой точки равна нулю. Через неё проходит так называемая мгновенная ось, относительно которой тело совершает только вращение. Положение мгновенной оси со временем меняется.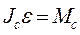 , (1)
, (1)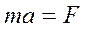 и
и 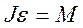 (2)
(2) .
. . С учетом уравнений (2) и ускорения
. С учетом уравнений (2) и ускорения 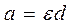 получим
получим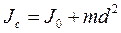 . (3)
. (3)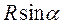 . Тогда момент силы тяжести М =
. Тогда момент силы тяжести М =  . Другие силы N и Fсц (нормального давления и сцепления) вращающего момента силы не создают
. Другие силы N и Fсц (нормального давления и сцепления) вращающего момента силы не создают  и углового ускорения
и углового ускорения  , получим
, получим 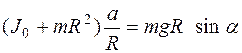 . Откуда формула для экспериментального определения момента инерции тела относительно оси О, проходящей через центр масс, будет иметь вид
. Откуда формула для экспериментального определения момента инерции тела относительно оси О, проходящей через центр масс, будет иметь вид
 . (4)
. (4)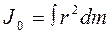 . Для кольца получим Jк = m R2; для шара
. Для кольца получим Jк = m R2; для шара 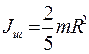 ; для диска
; для диска  .
.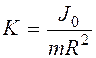 , которое не зависит ни от массы, ни от радиуса, а является параметром формы тела. Теоретическое значение для кольца Кк = 1, для диска Кд = 0, 5, для шара Кш = 0, 4. Из формулы (4)
, которое не зависит ни от массы, ни от радиуса, а является параметром формы тела. Теоретическое значение для кольца Кк = 1, для диска Кд = 0, 5, для шара Кш = 0, 4. Из формулы (4)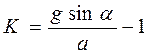 . (5)
. (5) . Но здесь неизвестна начальная скорость V 0, с которой исследуемое тело пересекает луч первого фотоэлемента, включающий секундомер. Но установка (рис.3) имеет семь секундомеров, измеряющих время движения тела до семи фотоэлементов. Это позволит решить систему семи уравнений алгебраически или лучше графически. Для этого представим уравнение в виде
. Но здесь неизвестна начальная скорость V 0, с которой исследуемое тело пересекает луч первого фотоэлемента, включающий секундомер. Но установка (рис.3) имеет семь секундомеров, измеряющих время движения тела до семи фотоэлементов. Это позволит решить систему семи уравнений алгебраически или лучше графически. Для этого представим уравнение в виде . (6)
. (6)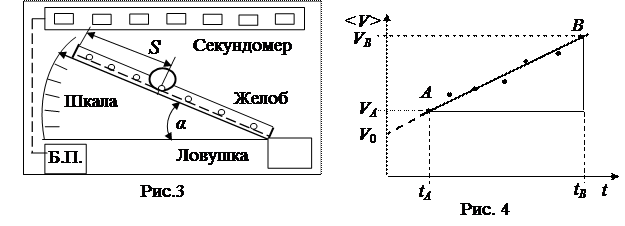
 . (7)
. (7)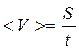 . Записать в табл.1.
. Записать в табл.1. с теоретическим значением. Оценить абсолютную погрешность
с теоретическим значением. Оценить абсолютную погрешность 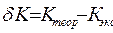 . Записать результат измерений
. Записать результат измерений 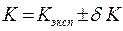 . Сделать выводы.
. Сделать выводы.


