ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ. .
 , импульсом силы является произведение силы на время ее действия , импульсом силы является произведение силы на время ее действия 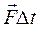 .) .)
Силы удара могут быть сравнительно большими, так как, согласно второму закону Ньютона, изменение импульса тела равно импульсу силы:
Закон сохранения импульса является важнейшим законом механики. Он позволяет рассчитать скорости тел после взаимодействия, даже не имея представления о силах взаимодействия. Существует две предельных идеализации реального удара: идеально упругий удар и абсолютно неупругий удар. При идеально упругом ударе тела в фазе сближения деформируются упруго, и часть кинетической энергии превращается в потенциальную энергию упругой деформации. Затем во второй фазе под действием упругих сил тела отталкиваются, форма тел восстанавливается, и потенциальная энергия деформации вновь превращается в кинетическую энергию. В результате кинетическая энергия сохраняется. При абсолютно неупругом ударе тела деформируются пластически. Удар заканчивается на фазе сближения, и затем тела движутся совместно, как одно целое. Это является признаком неупругого удара. Так как часть кинетической энергии превращается в работу пластической деформации, во внутреннюю энергию, то кинетическая энергия не сохраняется. Диссипацию, то есть рассеяние кинетической энергии, характеризуют коэффициентом восстановления энергии. Он равен отношению кинетической энергии обоих тел после удара к их энергии до удара:
Для идеально упругого удара К= 1, в других случаях К< 1. Рассмотрим прямой центральный удар двух шаров, при котором скорости шаров направлены по линии центров масс и точка соприкосновения тоже находится на этой линии. Пусть правый шар массы т 1 со скоростью V1 налетает на покоящийся, V 2 = 0, левый шар массы т 2. Закон сохранения импульса для упругого и неупругого ударов в проекции на направление движения правого шара (рис. 1) будет иметь вид:
Скорости шаров определим по углам отклонения их нитей подвеса от вертикали. Приведем пример для правого шара. При движении от крайнего положения с высоты h потенциальная энергия переходит в кинетическую энергию. Согласно закону сохранения механической энергии
Откуда Высота падения
Значение коэффициента восстановления энергии можно определить по углам отклонения шаров. Если подставить в формулу (2) скорости шаров, то получим для упругого и неупругого ударов:
Для неупругого удара теоретическое значение коэффициента восстановления энергии можно определить, подставив в формулу (2) скорость шаров после удара из (4):
|

 , и при малом времени удара D t сила удара может быть большой. В этом случае действием внешних сил на время удара можно пренебречь и считать систему соударяющихся тел замкнутой. Для замкнутой системы тел выполняется закон сохранения импульса: в замкнутой системе тел сумма импульсов тел постоянна, или сумма импульсов тел до взаимодействия равна сумме импульсов тел после взаимодействия:
, и при малом времени удара D t сила удара может быть большой. В этом случае действием внешних сил на время удара можно пренебречь и считать систему соударяющихся тел замкнутой. Для замкнутой системы тел выполняется закон сохранения импульса: в замкнутой системе тел сумма импульсов тел постоянна, или сумма импульсов тел до взаимодействия равна сумме импульсов тел после взаимодействия: или
или 
 . (1)
. (1) . (2)
. (2) ; (3)
; (3)
 . (4)
. (4)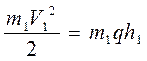 . (5)
. (5)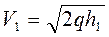 .
. связана с углом отклонения
связана с углом отклонения  нити длиной l соотношением
нити длиной l соотношением  . Для малых углов отклонения
. Для малых углов отклонения  . Тогда скорость шара перед ударом будет пропорциональна углу отклонения
. Тогда скорость шара перед ударом будет пропорциональна углу отклонения  . По таким же формулам можно определить скорости других шаров. Подставив их в уравнения (3) и (4), получим уравнения, проверяемые экспериментально:
. По таким же формулам можно определить скорости других шаров. Подставив их в уравнения (3) и (4), получим уравнения, проверяемые экспериментально: , (6)
, (6) . (7)
. (7) ; (8)
; (8)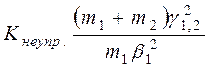 . (9)
. (9) . (10)
. (10)


