Введение. Рассмотрим движение механической системы, состоящей из вращающегося легкого блока, через который перекинута нить с привязанными грузами массами m1и т2(т1 <
Рассмотрим движение механической системы, состоящей из вращающегося легкого блока, через который перекинута нить с привязанными грузами массами m 1и т 2(т 1 < т 2) (рис. 1).
Если нить нерастяжимая, то ускорения грузов
(3)
Разность сил натяжения (T 2 – Т 1 ) зависит от меры инертности блока (момента инерции) и трения в подшипниках блока. В предельном случае отсутствия сил трения и нулевой массы блока и нити Т 2 = Т 1 , Поэтому а ускорение свободного падения
Учтем влияние сил трения в подшипниках оси блока (пренебрегая массой блока). Введем в уравнение (3) вместо разности Т 2– Т 1«эффективную» силу сопротивления F.
При сухом трении в подшипниках и незначительном изменении массы грузов m 1и m 2 в первом приближении можно считать, что отношение
Кинематическая связь ускорения а грузов с угловым ускорением β блока при отсутствии проскальзывания нити а = β R, (7) где R – радиус блока. При равноускоренном движении угол поворота блока φ при начальной угловой скорости ω о = 0
j. (8)
Из формул (7) и (8) следует
|
Запишем второй закон Ньютона в векторной форме для движения грузов
(1)
. Спроецируем векторные уравнения (1) на направление ускорения движения каждого груза.
(2)
Из уравнений (2) получим
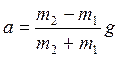, (4)
. (5)
, (6)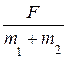
не зависит от масс грузов, а ускорение а зависит от величины k = (т 2 – m 1 )/ (m 1 + m 2 ).
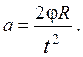(9)
