Краткая теория. Основной закон динамики вращательного движения твердого тела относительно неподвижной оси
Основной закон динамики вращательного движения твердого тела относительно неподвижной оси
связывает кинематическую характеристику движения – угловое ускорение Угловое ускорение характеризует изменение угловой скорости во времени и направлено, как и момент силы, вдоль оси вращения. Рис. 1. Момент M силы F
Угловое ускорение связано с касательной составляющей линейного ускорения а τ точки вращающегося тела соотношением
где r –- кратчайшее расстояние от этой точки до оси вращения. Моментом силы в общем случае называют векторную величину
где В уравнении (1) Момент инерции I характеризует распределение массы в твердом теле относительно оси вращения и является мерой инертности вращающегося тела. Момент инерции равен сумме произведений элементарных масс Δ mi, на которые мысленно разбито тело, на квадрат их расстояний до оси вращения I =Σ Δ mi ri . (5) Выражая Δ mi через плотность тела: Δ mi = ρ Δ Vi, где Δ Vi – элементарный объем тела, и переходя к пределу при Δ Vi → 0, получим
Формула (6) позволяет теоретически найти момент инерции любого тела. Например, момент инерции тонкого однородного стержня длиной l и массой т относительно оси, проходящей перпендикулярно стержню через его центр, I = т l 2 / 12. Теорема Штейнера устанавливает связь между моментом инерции Iс твердого тела относительно оси, проходящей через центр инерции, и моментом инерции относительно другой оси, параллельной первой I = Iс + та2 , (7) где а – расстояние между осями, т – масса тела. В настоящей работе экспериментально находится момент инерции маятника Обербека (рис.2). Он состоит из блока радиусом R, который может вращаться вокруг неподвижной горизонтальной оси. К блоку прикреплены симметрично относительнооси стержни, на каждом из которых могут свободно перемещаться грузы массами m 1, что дает возможность изменять момент инерции маятника. Грузы m 1 устанавливаются на одинаковом расстоянии от оси, так что центр инерции всей вращающейся части маятника находится на оси вращения.
.
Рис. 2. Маятник Обербека
К концу нити прикреплен груз массой m. Из закона динамики вращательного движения следует
Момент силы М, создающийся силой натяжения нити, исходя из (4)
где α – угол между вектором Запишем второй закон Ньютона для поступательного движения груза m в проекции на направление ускорения а,
В этой формуле сила натяжения нити T, действующая на груз, по модулю равна силе натяжения нити, действующей на блок в формуле (9) (поэтому они обозначены одинаково). Это справедливо, если массой нити можно пренебречь по сравнению с массой груза т. Из (9) и (10) получим
Тогда из (3) следует, (12)
Подставляя (11)и(12)в (8), получим Из этой формулы следует, что ускорение (а) не зависит от времени, так как все остальные величины в этом уравнении постоянны, значит, движение маятника будет равноускоренным и при нулевой начальной скорости.
где h – путь, пройденный грузом т за время t. В данной работе измеряется время одного полного оборота блока, и за это время груз массой m пройдет путь h =2π R. (15) Подставив (14) и (15) в (13), получим формулу для вычисления момента инерции маятника
(16)
Момент инерции маятника Обербека будет изменяться при изменении расстояния r от оси вращения маятника до центров грузов массами m 1, перемещаемых вдоль стержней. Согласно теореме Штейнера (7)
где Ic – момент инерции всей вращающейся части маятника при условии, что центры грузов m 1находились бы на оси вращения. Из (17) следует, что зависимость
|


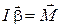 (1)
(1) с динамическими характеристиками – моментом силы
с динамическими характеристиками – моментом силы  и моментом инерции I (рис. 1).
и моментом инерции I (рис. 1). . (2)
. (2)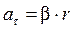 , (3)
, (3) , (4)
, (4) – сила, лежащая в плоскости, перпендикулярной оси вращения;
– сила, лежащая в плоскости, перпендикулярной оси вращения;  – вектор, соединяющий точку на оси c точкой приложения силы.
– вектор, соединяющий точку на оси c точкой приложения силы. (6)
(6)
 . (8)
. (8)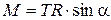 , (9)
, (9)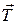 и отрезком R на рис. 2, равный 90°; sin α = 1.
и отрезком R на рис. 2, равный 90°; sin α = 1.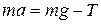 . (10)
. (10)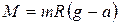 . (11)
. (11)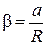 Тангенциальное (касательное) ускорение точек участков нити, намотанной на блок, и точек на ободе блока равны, если нет проскальзывания нити по блоку, и равны ускорению груза m, если нить нерастяжима.
Тангенциальное (касательное) ускорение точек участков нити, намотанной на блок, и точек на ободе блока равны, если нет проскальзывания нити по блоку, и равны ускорению груза m, если нить нерастяжима. (13)
(13) (14)
(14)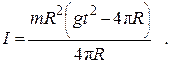
 , (17)
, (17)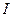 от
от 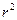 – линейная. В рассмотренной теории движения маятника Обербека не учитывались силы трения в подшипниках оси блока и сопротивление воздуха. Пренебрежение действием этих сил является главной причиной систематической погрешности измерения момента инерции.
– линейная. В рассмотренной теории движения маятника Обербека не учитывались силы трения в подшипниках оси блока и сопротивление воздуха. Пренебрежение действием этих сил является главной причиной систематической погрешности измерения момента инерции.


