Задания для отчета по лабораторной работе. 1. Два маленьких шарика массой m = 10 г каждый скреплены тонким невесомым стержнем длиной l = 20 см
1. Два маленьких шарика массой m = 10 г каждый скреплены тонким невесомым стержнем длиной l = 20 см. Определить момент инерции 2. Два шара массами m и 2m (m = 10 г) закреплены на тонком невесомом стержне длиной l = 40 см так, как это указано на рис. 4. Определить момент инерции 3. Два шара массами 2m и m (m = 20 г) закреплены на тонком невесомом стержне длиной l = 1 м так, как это показано на рис. 5 Определить момент инерции
Рис. 4 (к задаче 2) Рис. 5 (к задаче 3)
4. Определить момент инерции трехатомной молекулы H2O (рис. 6) относительно оси y, проходящей через центр масс молекулы. Межъядерное расстояние AB обозначено d = 0, 097 нм, α = 104о30' . 5. Определить момент инерции трехатомной молекулы SO2 (рис. 6) относительно оси x, проходящей через центр масс молекулы (d = 0, 145 нм, α = 124о).
Рис. 6 (к задаче 6)
6. Определить момент инерции тонкого однородного стержня длиной l = 30 см и массой m = 100 г относительно оси, перпендикулярной стержню и проходящей через точку, отстоящую от конца стержня на 1/3 его длины. Определить момент инерции a = 20 см от одного из его концов.
Рис. 7 (к задаче 7) 8. Вычислить момент инерции J проволочного прямоугольника со сторонами a = 12 см и b = 16 см относительно оси, лежащей в плоскости прямоугольника и проходящей через середины малых сторон. Масса равномерно распределена по длине проволоки с линейной плотностью 0, 1 кг/м. 9. Определить момент инерции 10. Определить момент инерции 11. Диаметр диска d = 20 см, масса m = 800 г. Определить момент инерции 12. Найти момент инерции 13. Определить момент инерции 14. В однородном диске массой m = 1 кг и радиусом R = 30 см вырезано круглое отверстие диаметром d =20 см, центр которого находится на расстоянии l = 15 см от оси диска (рис. 8). Найти момент инерции 15. На однородный сплошной цилиндр массой M и радиуса R плотно намотана легкая нить, к концу которой прикреплен груз массой m (рис.9). В момент времени t = 0 система пришла в движение. Пренебрегая трением в оси цилиндра, найти зависимость от времени модуля угловой скорости цилиндра.
Рис. 8 (к задаче 14) Рис. 9 (к задаче 15)
16. Через неподвижный блок массой m = 0, 2 кг перекинут шнур, к концам которого подвесили грузы массами m 1 = 0, 3 кг и m 2 = 0, 5 кг. Определить силы T 1и T 2 натяжения нити по обе стороны блока во время движения грузов, если масса блока равномерно распределена по ободу. 17. Через блок, имеющий форму диска, перекинут шнур. К концам шнура привязали грузы массой m 1 = 100 г и m 2 = 110 г. С каким ускорением будут двигаться грузы, если масса блока m = 400 г. Трение при вращении блока ничтожно мало. 18. Два тела массами m 1 = 0, 25 г и m 2 = 0, 15 г связаны тонкой нитью, переброшенной через блок (рис. 10). Блок укреплен на краю горизонтального стола, по поверхности которого скользит тело массой m1. С каким ускорением движутся тела, и каковы силы T 1 и T 2 натяжения нити по обе стороны блока? Коэффициент трения µ тела о поверхность стола равен 0, 2. Масса m блока равна 0, 1 г, и ее можно считать равномерно распределенной по ободу. Массой нити и трением в подшипниках оси блока пренебречь. 19. Однородный сплошной цилиндр массой m = 1 кг висит в горизонтальном положении на двух намотанных на него невесомых нитях (рис.11). Цилиндр отпускают без толчка. а) За сколько времени t цилиндр опустится на расстояние y =50 см? б) Какое натяжение F испытывает при опускании цилиндра каждая из нитей?
Рис. 10 (к задаче 18) Рис. 11 (к задаче 19)
|

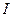 системы относительно оси, перпендикулярной стержню и проходящей через центр масс.
системы относительно оси, перпендикулярной стержню и проходящей через центр масс.

 тонкого однородного стержня длиной l = 60 см и массой m = 100 г относительно оси, перпендикулярной ему и проходящей через точку стержня, удаленную на
тонкого однородного стержня длиной l = 60 см и массой m = 100 г относительно оси, перпендикулярной ему и проходящей через точку стержня, удаленную на 7. На концах тонкого однородного стержня длиной l и массой 3 m прикреплены маленькие шарики массами m и 2 m. Определить момент инерции
7. На концах тонкого однородного стержня длиной l и массой 3 m прикреплены маленькие шарики массами m и 2 m. Определить момент инерции 






