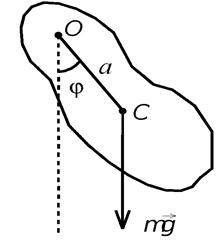
Краткая теория. Физический маятник – твердое тело, которое может совершать колебания под действием силы тяжести относительно неподвижной оси O(рис
Физический маятник – твердое тело, которое может совершать колебания под действием силы тяжести относительно неподвижной оси O(рис. 1).
Рис. 1. Физический маятник
Запишем основное уравнение динамики вращательного движения. . I β = М, (1) где I – момент инерции маятника;
M = - mga × sinj,, (2) где т – масса маятника, g –- ускорение свободного падения, а –- расстояние от оси вращения до центра тяжести. Уравнение движения (1) с учетом (2) примет вид I j = - mga × sinα где ω о2 = (mga)/I, тогда получим уравнение:
Уравнение (3) является линейным дифференциальным уравнением относительно функции φ (t). Если амплитуда колебаний физического маятника не мала, дифференциальное уравнение (3) не будет линейным. Для больших углов отклонений маятника период Т начинает зависеть от амплитуды колебаний φ m . Эту зависимость можно представить суммой бесконечного ряда, первые слагаемые которого равны
При малых колебаниях угол φ мал, поэтому sinφ ≈ φ и уравнение (3) становится дифференциальным уравнением гармонических колебаний
Решение этого уравнения: j = j m cos(ω 0t + α), (6)
где α - начальная фаза колебаний, ω о = 2π /Т - циклическая частота колебаний. Запишем формулу периода малых колебаний, как
Получим зависимость периода малых колебаний от расстояния а. Момент инерции, согласно теореме Штейнера, равен
где Iс - момент инерции маятника относительно оси, проходящей через центр масс. Подставляя (8) в (7), получим
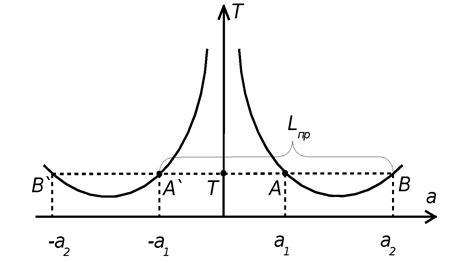
Согласно этой формуле период колебаний Т одинаков при двухразличных значениях а (рис. 2): Т 1 = Т 2 при
Подставим (10) в формулу (9). Получим
Величина называется приведенной длиной физического маятника. Сравнивая формулы (11) и (7) получим
Формула для периода малых колебаний маятника будет иметь следующий вид
В данной работе с помощью физического маятника находится ускорение свободного падения g, которое исходя из уравнения (14),
Приведенная длина Для уменьшения погрешности измерения в эксперименте измеряют период колебаний маятника относительно осей, находящихся по обе стороны от центра тяжести. На рис. 2 представлена теоретическая зависимость периода колебаний от параметра a, которая зеркально симметрична относительно оси Т.
Рис. 2. Зависимость периода колебаний маятника от параметрa a На рисунке приведенная длина маятника L np = a 1 + a 2 равна расстоянию между точками А ̀ В или В̀ А.
|

 – угловое ускорение, φ – угол отклонения маятника от положения равновесия, М - сумма проекций моментов сил на направление оси вращения. Если момент сил трения много меньше момента силы тяжести, то
– угловое ускорение, φ – угол отклонения маятника от положения равновесия, М - сумма проекций моментов сил на направление оси вращения. Если момент сил трения много меньше момента силы тяжести, то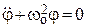 . (3)
. (3)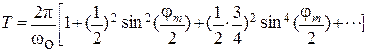 . (4)
. (4)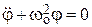 . (5)
. (5)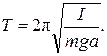 (7)
(7)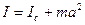 , (8)
, (8) (9)
(9)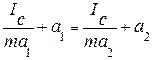 , откуда
, откуда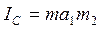 . (10)
. (10)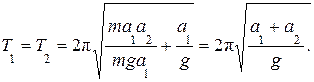 (11)
(11)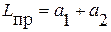 (12)
(12)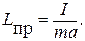 (13)
(13)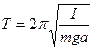 . (14)
. (14) . (15)
. (15)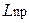 находится из формулы (12), в которой а 1и а 2определяются из графика зависимости Т от а, построенного на основе результатов эксперимента.
находится из формулы (12), в которой а 1и а 2определяются из графика зависимости Т от а, построенного на основе результатов эксперимента.