Порядок выполнения работы. Задание I. Определение коэффициента упругости пружин
Задание I. Определение коэффициента упругости пружин
1. Подвесьте пружины с помощью балки 17 на оси блока 13 и закрепите на другом конце пружин груз т 1(см. рис. 2). 2. Измерьте линейкой расстояние x 1от основания стойки до нижнего края груза. 3. Измените массу груза на величину Δ m и измерьте новое расстояние х 2. Данные занесите в табл. 1. Рассчитайте коэффициент упругости пары пружин по формуле
где g = 9, 81 м/с – ускорение свободного падения. 4. Повторите измерения несколько раз. Рассчитайте среднее значение k пар . Данные занесите в табл. 1.
Таблица 1
Задание II. Определение момента инерции методом крутильных колебаний 1. Подготовьте измерительную систему ИСМ-1 к работе: подключите датчик угла поворота стола блока к разъему №1на задней стенке прибора, переключатель 1 поставьте в положение «К1», переключатель 4 – в положение «2», переключатель 5 – в положение «цикл», переключатель 8 – в положение «+» или переключатель 9 – в среднее положение. Включите питание модуля. 2. Накрутите нить (1, 5 оборота) на шкив стола, диаметр которого D = 50мм (рис. 3), прикрепите к концам нити пружины. Закрепите пружины на осях 12 нижнего блока стойки 10. 3. Поверните стол так, чтобы в свободном положении указатель угла поворота стола находился вблизи нулевого деления шкалы 16. 4.
Нажмите кнопку 7 «готов» и приведите стол в колебательное движение с амплитудой 40 – 60 градусов. Рис.3. Определение момента инерции маятника
5. Считайте с индикатора время одного полного колебания T.
(19)
где R – радиус шкива стола (R=D/ 2), k пар – коэффициент упругости двух пружин, соединенных параллельно. Данные занесите в табл. 2. Повторите измерения 5 – 7 раз. Таблица 2
Задание III. Проверка теоремы Штейнера 1. Поместите в центре стола два цилиндрических груза 18 массой т цпо 500 г один над другим (точная масса грузов выгравирована на нижнем торце грузов). Повторите измерения момента инерции системы I сис (по п. 3 – 6 в задании II). 2. Рассчитайте момент инерции цилиндров по формуле I ц = I сис – I о, (21) где I 0 - момент инерции не нагруженного стола, измеренный в задании II. 3. Рассчитайте теоретический момент инерции цилиндров I теор относительно оси цилиндров по формуле
где т ц – суммарная масса цилиндров, R ц – радиус цилиндров (R ц = 24 мм). Данные занесите в табл. 3. 4. Переместите цилиндры на одинаковое расстояние Δ х относительно оси вращения (шаг отверстий на вращающемся столе Δ х =20мм).Измерьте период колебаний m 2 системы, соответствующий новому положению цилиндров. Данные занесите в табл. 3.
Таблица 3
5. Рассчитайте момент инерции системы I сис по формуле
где k пар – коэффициент упругости пары пружин (см. задание I), R –- радиус шкива стола.
где I0 – момент инерции не нагруженного стола (см. задание II), т ц – суммарная масса цилиндров, R ц – радиус цилиндров (R ц = 24 мм). 7. Повторите измерения и расчеты по п. 1– 6 для всех положений цилиндров. Данные занесите в табл. 3. 8. Постройте график зависимости момента инерции I сиси I теор от квадрата расстояния от оси вращения до центра грузов Δ х 2. Контрольные вопросы 1. Дайте определение динамических характеристик вращательного движения: момента силы – М, момента инерции – I, момента импульса – L. 2. Запишите аналитические выражения для момента инерции частицы и твердого тела. Как производится расчет момента инерции обруча, стержня, диска? 3. В чем состоит суть теоремы Штейнера? 4. Получите основное уравнение динамики вращательного движения. 5. Получите уравнение колебаний крутильного маятника. 6. Как рассчитать период колебаний крутильного маятника?
|

 (18)
(18) = т 1– m 2, кг
= т 1– m 2, кг

 6. Рассчитайте момент инерции ненагруженного стола по формуле
6. Рассчитайте момент инерции ненагруженного стола по формуле (22)
(22) (23)
(23)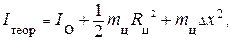 6. Рассчитайте теоретический момент инерции системы по формуле
6. Рассчитайте теоретический момент инерции системы по формуле


