КРАТКАЯ ТЕОРИЯ. Моментом инерции материальной точки относительно какой-либо оси называется произведение ее массы на квадрат расстояния до этой оси:
Моментом инерции материальной точки относительно какой-либо оси называется произведение ее массы на квадрат расстояния до этой оси:
Моментом инерции твердого тела относительно какой либоосиназывается сумма моментов инерции всех точек тела относительно этой же оси:
Момент инерции тела относительно данной оси, не зависит от характера движения тела, а зависит от массы тела, его размеров, формы, т.е. от распределения массы относительно оси вращения. Момент инерции тел правильной геометрической формы может быть вычислен теоретически. Момент инерции тела является физической величиной, характеризующей инертность тела при вращательном движении: тело с большим моментом инерции будет иметь меньшее угловое ускорение при том же действующем моменте сил. Расчет момента инерции тел. В формуле (2) элементарная масса
Если плотность тела постоянная, ее можно вывести за знак суммы:
Для сплошного тела соотношения (3) и (4) являются приближенными, причем тем более точными, чем меньше элементарные объемы
Причем интеграл берется по всему объему, а величины r и r являются функциямикоординат. В качестве примера найдем момент инерции однородного шара (рис. 1).
Схематическое изображение однородного шара (R – радиус шара, r – радиус бесконечно малого элемента, z – расстояние)
При вычислении момента инерции шара его разбивают на бесконечно большое число бесконечно малых элементов с массами dm (см. рис. 1), тогда масса шара равна:
Момент инерции шара равен:
Формулы для расчета момента инерции тел правильной формы массы m относительно осей, проходящих через центр масс даны в таблице 1. Если же тело имеет сложную форму (маховое колесо, коленчатый вал, винт и т.д.), то теоретически определить момент инерции трудно. В таких случаях момент инерции определяют экспериментальным путем, например, используя крутильные колебания. Таблица 1. Таблица моментов инерции для однородных тел простейшей формы
Схема крутильного маятника изображена на рис. 2
Рис. 2 Схема крутильного маятника: (R – радиус цилиндра, l – длина проволоки, φ – уголповорота)
Крутильный маятник представляет собой упругую проволоку с закрепленным верхним концом к нижнему концу, которой жестко присоединено изучаемое тело. Поворачивая тело на угол j, мы создаем в проволоке возвращающий момент упругой силы Муп, который по закону Гука пропорционален деформации кручения j
где ¦ - модуль кручения, который зависит от параметров проволоки.
где d - диаметр проволоки; l - длина проволоки; N - модуль сдвига материала проволоки. По второму закону Ньютона, момент упругой силы создает угловое ускорение
Таким образом, свободное вращение крутильногомаятника при пренебрежении силами трения, будет описываться дифференциальными уравнениями, объединяющими второй закон Ньютона и закон Гука.
Интегрируя эти уравнения, получаем его решение
Следовательно, при допустимости сделанныхнами упрощений, маятникбудет совершать гармонические колебания с периодом колебаний
|



 , равна произведению плотности тела
, равна произведению плотности тела  в данной точке на соответствующий элементарный объем
в данной точке на соответствующий элементарный объем  :
:  . Следовательно, момент инерции можно представить в виде:
. Следовательно, момент инерции можно представить в виде:

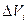 и соответствующие им элементарные массы
и соответствующие им элементарные массы 






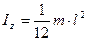





 пропорциональное этому моменту.
пропорциональное этому моменту.






