Уравнение  описывает изменение движения протяженного тела под действием силы при отсутствии деформации и оно движется. Для точки оно справедливо всегда. поэтому его можно рассматривать как основной закон движения материальной точки: ускорение материальной точки пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки. В механике Ньютона масса не зависит от характеристик движения,
описывает изменение движения протяженного тела под действием силы при отсутствии деформации и оно движется. Для точки оно справедливо всегда. поэтому его можно рассматривать как основной закон движения материальной точки: ускорение материальной точки пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки. В механике Ньютона масса не зависит от характеристик движения,  ,
, 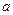 ускорение
ускорение  ;
; 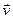 —скорость точки, тогда
—скорость точки, тогда  или
или
 (**).
(**).
Вектор 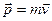 называют импульсом материальной точки. В теоретической механике(а раньше и в физике) вектор
называют импульсом материальной точки. В теоретической механике(а раньше и в физике) вектор  называют количеством движения. Импульс одна из важнейших динамических характеристик материальной точки
называют количеством движения. Импульс одна из важнейших динамических характеристик материальной точки
В форме (**) основной закон динамики материальной точки утверждает, что скорость изменения импульса материальной точки равна действующей на нее силе. В этом состоит (согласно современной терминологии) второй закон Ньютона.
Основной закон динамики материальной точки выражает принцип причин в классической механике, т.к. устанавливает однозначную связь между изменением со временем состояния движения и положения материальной точки в пространстве и действия на нее силы. Закон позволяет по начальному состоянию точки (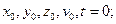 ) и действующей силы рассчитать состояние материальной точки в любой последующий момент времени.
) и действующей силы рассчитать состояние материальной точки в любой последующий момент времени.
На основании обобщения опытных фактов был установлен важный принцип независимости действия сил: если на материальную точку одновременно действует несколько сил, то каждая из них, сообщает материальной точке такое же ускорение, как если бы других сил не было. Т.о.
 ;
; 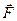 —результирующая сила;
—результирующая сила;
Основной закон можно переписать в виде:
 ;
;
вектор 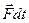 называется элементарным импульсом силы за малый промежуток времени
называется элементарным импульсом силы за малый промежуток времени  её действия. Т.о. из основного закона и принципа независимости действия сил следует, что изменение импульса материальной точки за малый промежуток времени
её действия. Т.о. из основного закона и принципа независимости действия сил следует, что изменение импульса материальной точки за малый промежуток времени  равно элементарному импульсу результирующих всех сил, действующих на эту точку за тот же
равно элементарному импульсу результирующих всех сил, действующих на эту точку за тот же  .
.
 Изменение импульса за конечный промежуток времени от
Изменение импульса за конечный промежуток времени от  до
до 

—импульс силы;
если  то
то  ,
,  среднее значение силы за
среднее значение силы за  .
.
 —импульс силы;
—импульс силы;

 описывает изменение движения протяженного тела под действием силы при отсутствии деформации и оно движется. Для точки оно справедливо всегда. поэтому его можно рассматривать как основной закон движения материальной точки: ускорение материальной точки пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки. В механике Ньютона масса не зависит от характеристик движения,
описывает изменение движения протяженного тела под действием силы при отсутствии деформации и оно движется. Для точки оно справедливо всегда. поэтому его можно рассматривать как основной закон движения материальной точки: ускорение материальной точки пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки. В механике Ньютона масса не зависит от характеристик движения,  ,
, 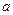 ускорение
ускорение  ;
; 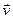 —скорость точки, тогда
—скорость точки, тогда  или
или (**).
(**).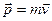 называют импульсом материальной точки. В теоретической механике(а раньше и в физике) вектор
называют импульсом материальной точки. В теоретической механике(а раньше и в физике) вектор  называют количеством движения. Импульс одна из важнейших динамических характеристик материальной точки
называют количеством движения. Импульс одна из важнейших динамических характеристик материальной точки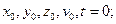 ) и действующей силы рассчитать состояние материальной точки в любой последующий момент времени.
) и действующей силы рассчитать состояние материальной точки в любой последующий момент времени. ;
; 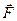 —результирующая сила;
—результирующая сила; ;
;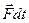 называется элементарным импульсом силы за малый промежуток времени
называется элементарным импульсом силы за малый промежуток времени  её действия. Т.о. из основного закона и принципа независимости действия сил следует, что изменение импульса материальной точки за малый промежуток времени
её действия. Т.о. из основного закона и принципа независимости действия сил следует, что изменение импульса материальной точки за малый промежуток времени  Изменение импульса за конечный промежуток времени от
Изменение импульса за конечный промежуток времени от  до
до 

 то
то  ,
,  среднее значение силы за
среднее значение силы за  .
.


