Решение. У нас имеются две гипотезы: Но и Н1
У нас имеются две гипотезы: Но и Н1. Н0: различия между Fэ(х) и F(x) несущественны, то есть данные выборки согласуются с равномерным распределением на отрезке [0, 10]. Н1: противоположная гипотезе Н0. Функция распределения случайной величины, равномерно распределенной на отрезке [0, 10], имеет вид:
Заполним таблицу. · Первые два столбца взяты из условия. · Числа 3-его столбца получается делением на сумму всех ni. · Каждое число 4-го столбца равно сумме числа из этой же строки 3-го столбца и предыдущего числа 4-го столбца. · Числа 5 и 6 столбца получаются, исходя из формул.
Выявим наибольшее число последнего столбца = 0, 1. По значению статистики: λ = 0, 1* По уровню значимости, указанной в условии задачи, из специальной таблицы находим граничную точку λ α = 1, 358. Так как λ < λ α (1< 1, 358); то мы принимаем гипотезу Н0 на уровне значимости α =0, 05. Данные выборки согласуются с равномерным распределением на указанном отрезке [0, 10].
2. В таблице указано распределение ущерба в двух портфелях страховых договоров.
На уровне значимости α =0, 05 с помощью λ -критерия Колмогорова-Смирнова проверить гипотезу о том, что распределение ущерба в этих двух портфелях одинаково (Н0).
|



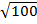 = 1.
= 1.


