ЛАБОРАТОРНАЯ РАБОТА №4
“МЕХАНИКА”
Методическое пособие составлено для лабораторных работ, выполняемых на стандартном оборудовании типа ФПМ, по разделу “Механика” курса общей физики. Особенностью пособия является включение в описания лабораторных работ раздела “Вопросы и задания для учебно-исследовательской работы студентов”. В приложении приводится описание метода линеаризации функции, который широко используется в физических исследованиях для сравнения эксперимента с теорией.
Составитель В.Я.Мартенс
Л А Б О Р А Т О Р Н А Я Р А Б О Т А N 1.1
ИЗУЧЕНИЕ КИНЕМАТИКИ И ДИНАМИКИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ НА МАШИНЕ АТВУДА
ЦЕЛЬ РАБОТЫ: изучение кинематики и динамики поступательного движения.
К Р А Т К А Я Т Е О Р И Я При поступательном движении все точки тела движутся одинаково, и его движение задается и изучается так же, как движение одной точки. Основными кинематическими характеристиками движущейся точки являются скорость и ускорение, которые определяются по законам динамики. Рассмотрим движение двух грузов 1 и 2, соединенных нитью 3, перекинутой через блок 4 (рис.1.1.1.).
Массы грузов одинаковы (М 1 = М 2= М), поэтому для того, чтобы вывести систему из равновесия, на груз 2 кладут перегрузок 5 массой m. На каждый груз действуют две силы: сила тяжести M g или (M + m) g и сила реакции нити T 1или T 2. Под действием этих сил грузы будут двигаться поступательно в противоположных направлениях. Если учесть, что нить нерастяжима, то ускорения обоих грузов будут одинаковы по величине (a 1= a 2= a) и противоположны по направлениям. Ускорение грузов а может быть определено из второго закона Ньютона (основного закона динамики поступательного движения), который можно записать для первого груза в виде M a = M g + T 1, (1) а для второго груза (M + m) a =(M + m) g + T 2. (2)
Если пренебречь силами трения, а также массами нити и блока, то силы реакции нити T 1 и T 2 равны по величине: T 1 = T 2 = T. С учетом этих упрощений запишем уравнения (1) и (2) в проекциях на вертикальную ось: Ma = T - Mg (3) (M + m) a =(M + m) g - T.
Исключив из системы (3) силу реакции Т, получим
a =
Из этого выражения видно, во-первых, что ускорение не зависит от времени (ни одна из величин, входящих в правую часть, не меняется во время движения грузов), что доказывает равноускоренный характер движения грузов. Во-вторых, видно, что изменить ускорение можно, меняя массу перегрузка m. В случае равноускоренного движения скорость грузов v и перемещение h, грузов за время t определяются уравнениями
v = v 0 + a t, h = v 0 t +
Так как начальная скорость v 0 = 0, то
v = a t, (5) h =
Соотношение (6) можно проверить экспериментально, сняв зависимость h от t. Зависимость h (t), как следует из (6), нелинейная. Поэтому для удобства экспериментальной проверки эту зависимость следует линеаризовать (см. Приложение), т.е. выявить такие новые переменные, зависимость между которыми была бы линейной. В нашем случае такими переменными являются h и t 2. Если график экспериментальной зависимости h = f 1(t 2) окажется прямой линией (в пределах погрешности измерений), проходящей через начало координат, то это будет означать, что зависимость (6) подтверждена экспериментально. Используя график линеаризованной зависимости h = f 1(t 2), можно определить величину ускорения а через угловой коэффициент прямой (см. Приложение). В нашем случае а =
где D(t 2)- произвольный отрезок на оси t 2 (приращение аргумента), D h - соответствующий отрезок на оси h (соответствующее приращение функции). Соотношение (4) также может быть проверено экспериментально. Если брать перегрузки массой m < < M, то
a = т.е. зависимость a = f 2(m) должна быть линейной. Значения ускорения a при различных m можно определить следующим образом. Снять зависимости h = f 1(t 2) для различных m и по графикам этих зависимостей по указанной выше методике определить соответствующие значения а. Если график экспериментальной зависимости a = f 2(m) окажется прямой линией (в пределах погрешности измерений), проходящей через начало координат, то это будет означать, что зависимость (4) подтверждена экспериментально, а следовательно, справедлив второй закон Ньютона, взятый за основу при выводе этого выражения. ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ Для экспериментальной проверки основных соотношений кинематики и динамики равноускоренного поступательного движения используется машина Атвуда (рис.1.1.2).
Машина Атвуда представляет собой систему двух одинаковых по массам грузов 1 и 2, соединенных нитью 3, перекинутой через легкий блок 4. Для приведения системы в движение на правый груз устанавливается кольцевой перегрузок 5. В комплекте имеется несколько перегрузков различной массы. Масса максимального перегрузка m = 4, 8 г. Если учесть, что масса каждого груза М = 80 г, то m /2 M На среднем кронштейне крепится фотодатчик 8, соединенный кабелем с электронным миллисекундомером 9. Ось фотодатчика совпадает с риской на корпусе кронштейна. На вертикальной стойке 7 укреплена линейка 10, по которой определяют начальное и конечное положение грузов, а следовательно и перемещение. Начальное положение определяют визуально по нижнему срезу груза, конечное положение - по риске на среднем кронштейне. Средний и нижний кронштейны (нижний кронштейн 11 представляет собой площадку с резиновым амортизатором, о который ударяется груз при остановке) имеют возможность свободного перемещения и фиксации на вертикальной стойке по всей ее длине. Миллисекундомер 9 предназначен для измерения времени движения. Он начинает отсчет времени при нажатии кнопки “ПУСК”. При этом электромагнитный фрикцион освобождает систему грузов, и она начинает движение. Отсчет времени прекращается при пересечении грузом 2 оптической оси фотодатчика 8.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Включить в сеть шнур питания установки. 2. Нажать на кнопку “СЕТЬ”, расположенную на лицевой панели миллисекундомера, при этом должны загореться лампочка фотодатчика и цифровые индикаторы миллисекундомера, сработать электромагнитный фрикцион и зафиксировать систему грузов. 3. Для снятия экспериментальной зависимости h = f 1(t 2) установить на правый груз один из перегрузков. 4. Нажав на кнопку “ПУСК” на миллисекундомере, переместить правый груз в верхнее положение, соответствующее начальному значению координаты х 1. Кнопку “ПУСК” отпустить. 5. Нажать на кнопку “СБРОС” и убедиться, что на индикаторах установились нули. 6. Нажать кнопку “ПУСК” и удерживать ее в нажатом состоянии до момента пересечения правым грузом оптической оси фотодатчика, соответствующей координате х 2. 7. Произвести отсчет времени t движения грузов по миллисекундомеру. Результаты измерений h = (x 2 - x 1)и t занести в табл.1.1.1 8. Повторить измерения по п.п. 4 - 7 не менее пяти раз. 9. Произвести измерения по пунктам 4 - 8 для других значений перемещений h. В колонку “Примечания” табл.1.1.1 занести значение массы перегрузка m. 10. Аналогичным образом снять экспериментальные зависимости h = f 1(t 2) для других (не менее трех) перегрузков различной массы m. При этом измерения времени при каждом значении h проводить однократно. Результаты измерений занести в табл.1.1.2. 11. Определить значения косвенно измеряемой величины t 2 экспериментальных зависимостей h = f 1(t 2) и занести их в табл.1.1.1 и табл.1.1.2. Для случая многократных измерений определить средние значения t 2 и занести их в табл.1.1.1. 12. По данным табл.1.1.1 рассчитать погрешности величины t 2 для первой и последней экспериментальных точек. Погрешности остальных экспериментальных точек можно считать промежуточными. 13. По данным табл.1.1.1 нанести экспериментальные точки на график в координатах h, t 2. На этот же график нанести доверительные интервалы величины t 2. 14. Провести график зависимости h = f 1(t 2). Убедиться, что график представляет собой прямую линию, проходящую через начало координат и через все доверительные интервалы. 15. В этой же системе координат построить графики трех других экспериментальных зависимостей h = f 1(t 2). При этом следует руководствоваться следующими соображениями. Поскольку первый график, соответствующий многократным измерениям, подтвердил справедливость уравнения (6), то графики для однократных измерений также должны представлять собой прямые линии. Проводить их надо через начало координат так, чтобы отклонения экспериментальных точек от прямой в ту и другую сторону были минимальны. 16. Сравнить наклон графиков при различных m. Используя графики и соотношение (7), определить величины ускорений а и занести их в табл.1.1.1 и табл.1.1.2. 17. По полученным экспериментальным результатам построить график зависимости a = f 2(m). Убедиться, что график представляет собой прямую линию, проходящую через начало координат, а отклонение экспериментальных точек от нее незначительны. 18. Определить с помощью выражения (5) скорость грузов в конце первой секунды для всех использованных перегрузков.
КОНТРОЛЬНЫЕ ВОПРОСЫ Сравнить между собой по величине силы M g, (M + m) g, Т 1 , Т 2 , когда система грузов неподвижна и когда она движется. Меняются ли во время движения скорость и ускорение грузов? Почему? О чем свидетельствует линейность экспериментальных зависимостей h = f 1(t 2) и a = f 2(m)? Как изменятся графики экспериментальных зависимостей h = f 1(t 2) и a = f 2(m), если увеличить массу грузов М? Как изменится характер движения грузов, если через некоторое время после начала движения перегрузок слетит с правого груза? Как изменится характер движения грузов, если через некоторое время после начала движения оборвется нить?
ВОПРОСЫ И ЗАДАНИЯ ДЛЯ УИРС Построить график экспериментальной зависимости a = f 2(m), используя метод наименьших квадратов (см. Приложение). Из углового коэффициента прямой определить ускорение свободного падения g. Определить погрешность ускорения свободного падения D g. Сравнить полученное значение g с теоретическим. Используя полученные в работе результаты, построить график зависимости v = f (t) для одного из перегрузков. Какой физический смысл имеет величина, равная площади фигуры, ограниченной указанным графиком, осью t и вертикальными прямыми t = t 1 и t = t 2? Как изменится график экспериментальной зависимости a = f 2(m), если условие m < < M будет нарушено? Как зависит сила реакции нити Т от массы грузов М и от массы перегрузка m? Почему масса блока машины Атвуда должна быть мала?
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА 1. Савельев И.В. Курс общей физики, т.1 - М.: Наука, 1986. С.17-45, 49-60. 2. Трофимова Т.И. Курс физики. - М.: Высшая школа, 1985. С.8-15. 3. Матвеев А.Н. Механика и теория относительности. - М.: Высшая школа, 1986. С.42-49, 105-115. 4. Голубин М.А., Хабибулин И.М., Шестопалова В.И. Введение в лабораторный практикум по физике. - Ставрополь, 1995, 32 с.
Л А Б О Р А Т О Р Н А Я Р А Б О Т А N 1.2
ИЗУЧЕНИЕ КИНЕМАТИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
ЦЕЛЬ РАБОТЫ: изучение кинематики вращательного движения твердого тела на примере равноускоренного вращения маятника Обербека.
К Р А Т К А Я Т Е О Р И Я Кинематика описывает конкретные механические движения, не интересуясь причинами, обусловливающими эти движения. Движение рассматриваемого объекта считается известным, если известны уравнения, позволяющие определить положение этого объекта по отношению к системе отсчета в любой момент времени. Способы задания движения твердого тела зависят от вида его движения, а число уравнений движения - от числа степеней свободы тела. Одним из простейших видов движения является вращательное движение твердого тела. При вращательном движении твердого тела вокруг неподвижной оси АВ (рис.1.2.1) тело имеет одну степень свободы.
Его положение определяется углом поворота j, а закон движения задается уравнением j = f (t). Основными кинематическими характеристиками являются угловая скорость w и угловое ускорение e тела. Угловая скорость - векторная величина, характеризующая быстроту вращения твердого тела. В общем случае w = d j /d t. Вектор w направлен вдоль оси вращения в сторону, определяемую правилом правого винта (в сторону, откуда поворот тела виден происходящим против часовой стрелки). Угловое ускорение - векторная величина, характеризующая быстроту изменения угловой скорости твердого тела. В общем случае e = d w /d t. Вектор e направлен вдоль оси вращения (в ту же сторону, что и w при ускоренном вращении и противоположно w - при замедленном). Для любой точки тела, отстоящей от оси на расстоянии r, ее линейная скорость v, тангенциальное ускорение a t, характеризующее изменение линейной скорости по численной величине, нормальное ускорение a n , характеризующее изменение линейной скорости по направлению, полное ускорение а определяются соотношениями:
v = w r, (1) a t = e r, (2) a n = w 2 r, (3) a = r
В случае равноускоренного вращения тела вокруг неподвижной оси, при котором e постоянно, угловая скорость w и угол поворота j определяются уравнениями w = w 0 + e t, (5) j = w 0 t +
где w 0 - начальная угловая скорость. В случае w 0 = 0 уравнение (5) и (6) могут быть переписаны в виде
w = e t, (7) j = Соотношение (8) можно проверить экспериментально, сняв зависимость j от t. Зависимость j (t), как следует из (8), нелинейная. Поэтому для удобства экспериментальной проверки эту зависимость следует линеаризовать (см. Приложение), т.е. выявить такие новые переменные, зависимость между которыми была бы линейной. В нашем случае такими переменными являются j и t 2. Если график экспериментальной зависимости j = f 2(t 2) окажется прямой линией (в пределах погрешности измерений), проходящей через начало координат, то это будет означать, что зависимость (8) подтверждена экспериментально. Используя график линеаризованной зависимости j = f 2(t 2), можно определить величину углового ускорения e через угловой коэффициент прямой (см. Приложение). В нашем случае e = где D(t 2) - произвольный отрезок на оси t 2 (приращение аргумента), D j -соответствующий отрезок на оси j (соответствующее приращение функции).
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
Для экспериментальной проверки уравнения кинематики равноускоренного вращательного движения твердого тела j = e t 2/2 в данной лабораторной работе используется маятник Обербека (рис.1.2.2). Он представляет собой крестовину, образованную четырьмя стержнями 1, закрепленными в бобышке 2 под прямым углом друг к другу. На каждом стержне могут свободно перемещаться и фиксироваться привески 3. При выполнении данной лабораторной работы привески рекомендуется снять. Крестовина может вращаться благодаря тому, что закреплена на одном конце оси подшипников. На другом конце этой оси закреплен двухступенчатый шкив 4 радиусами 21 и 42 мм. На шкив намотана нить 5, один конец которой прикреплен к шкиву. К другому концу нити, переброшенному через блок 6 (блок крепится на верхнем кронштейне 7), с помощью крючка подвешивается груз 8. Опускающийся груз тянет нить и равноускоренно раскручивает крестовину маятника Обербека. Теоретическое обоснование равноускоренного характера вращения крестовины приведено в руководстве к лабораторной работе N 1.3 “Изучение динамики поступательного и вращательного движения твердого тела”. Для измерения угла поворота маятника j может использоваться миллиметровая линейка 9. Если учесть, что путь h, пройденный грузом 8 и измеряемый по линейке 9, равен длине дуги, описываемой за это же время точкой на ободе шкива радиусом R, то
j =
Отсюда следует, что каждый мм пути груза при использовании шкива радиусом 21 мм соответствует углу поворота маятника на 4, 76•10 -2 рад, а при использовании шкива радиусом 42 мм - 2, 38•10 -2 рад. Для измерения времени используется электронный миллисекундомер 10. Он начинает отсчет времени при нажатии кнопки “ПУСК”. При этом электромагнитный фрикцион освобождает шкив 4 и маятник начинает раскручиваться. Отсчет времени прекращается при пересечении грузом 8 оптической оси фотодатчика 11.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Включить в сеть шнур питания экспериментальной установки. 2. Нажать на кнопку “СЕТЬ”, расположенную на лицевой панели миллисекундомера, при этом должны загореться лампочки фотодатчика и цифровые индикаторы миллисекундомера, сработать электромагнитный фрикцион и зафиксировать крестовину. 3. Нажав на кнопку “ПУСК” на миллисекундомере и вращая крестовину против часовой стрелки, перевести груз в положение, соответствующее первому значению угла j. Кнопку “ПУСК” отпустить. 4. Нажать на кнопку “СБРОС” и убедиться, что на индикаторах устанавливаются нули. 5. Нажать кнопку “ПУСК” и удерживать ее в нажатом состоянии до момента пересечения падающим грузом оптической оси фотодатчика. 6. Произвести отсчет времени хода маятника t по миллисекундомеру. Результаты измерений занести в табл.1.2.1. 7. Повторить измерения по п.п. 3 - 6 не менее пяти раз. 8. Произвести измерения по п.п. 3 - 7 для других значений угла j (не менее пяти). 9. Определить средние значения времени и квадрата времени поворота маятника на измеренные значения угла j. 10. Рассчитать случайную погрешность измерения t и t 2 для первой и последней экспериментальных точек. Погрешности остальных экспериментальных точек можно не рассчитывать, а выбрать промежуточными между погрешностями крайних. 11. Нанести экспериментальные точки на график в координатах j, t и на график в координатах j, t 2. На эти же графики нанести доверительные интервалы величин t и t 2. 12. Провести графики зависимостей j = f 1(t) и j = f 2(t 2). Убедиться, что график второй зависимости представляет собой прямую линию, проходящую через начало координат и через все доверительные интервалы. 13. Используя график зависимости j = f 2(t 2) и соотношение (9), вычислить величину углового ускорения e. 14. Для заданной преподавателем точки на стержне маятника Обербека определить с помощью выражений (1), (2), (3), (4), (7) нормальное, тангенциальное и полное ускорение, а также линейную скорость в конце первой секунды.
Таблица 1.2.1 Результаты измерения времени и угла поворота маятника Обербека
КОНТРОЛЬНЫЕ ВОПРОСЫ В чем сходство и отличия между уравнениями кинематики поступательного и вращательного движения твердого тела? Куда направлены w, e, v, a t, a n , a в маятнике Обербека? Зависят ли a t и a n точки от положения этой точки на стержне маятника Обербека? Зависят ли a t и a n от времени? Как зависит перемещение груза h от угла поворота j крестовины? О чем свидетельствует линейность экспериментальной зависимости j = f 2(t 2)?
ВОПРОСЫ И ЗАДАНИЯ ДЛЯ УИРС Построить график зависимости j = f 2(t 2), используя метод наименьших квадратов (см.Приложение). Определить погрешность углового ускорения e. Используя полученные в работе результаты, построить график зависимости w = f (t). Какой физический смысл имеет величина, равная площади фигуры, ограниченной указанным графиком, осью t и вертикальными прямыми t = t 1 и t = t 2? Каков характер вращения крестовины после того, как груз достигнет нижней точки пути, а кнопка “ПУСК” останется нажатой? Если бы по каким-либо причинам маятник вращался равномерно, то как выглядели бы графики зависимостей j = f 1(t) и j = f 2(t 2)? Если в данной работе начать отсчет времени через некоторое время после начала вращения маятника, т.е. w 0
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА 1. Савельев И.В. Курс общей физики, т.1 - М.: Наука, 1986. С. 41-48. 2. Трофимова Т.И. Курс физики. - М.: Высшая школа, 1985. С.10-12. 3. Матвеев А.Н. Механика и теория относительности. - М.: Высшая школа, 1986. С.46-53. 4. Голубин М.А., Хабибулин И.М., Шестопалова В.И. Введение в лабораторный практикум по физике. - Ставрополь, 1995, 32 с.
Л А Б О Р А Т О Р Н А Я Р А Б О Т А N 1.3
ИЗУЧЕНИЕ ДИНАМИКИ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
ЦЕЛЬ РАБОТЫ: изучение основных законов динамики поступательного и вращательного движения твердого тела на маятнике Обербека.
К Р А Т К А Я Т Е О Р И Я
Динамика изучает движение тел в связи с теми причинами, которые обусловливают тот или иной характер движения. Законы динамики можно изучать на экспериментальной установке, называемой маятником Обербека. Особенность этой экспериментальной установки заключается в том, что одна ее часть совершает поступательное движение, а другая - вращательное движение. Конструкция маятника Обербека описана в руководстве к лабораторной работе N 1.2 “Изучение кинематики вращательного движения”. Здесь же приводится только схема (рис.1.3.1), помогающая решить задачи данной работы. Обозначения на рис.1.3.1 те же, что и на рис.1.2.2. Причиной поступательного движения груза 8 является действие на него силы тяжести m g. Препятствует этому движению сила реакции нити T 1. Причиной вращательного движения крестовины маятника является действие на него силы реакции нити T 2. Результат действия силы во вращательном движении зависит не только от величины этой силы, но и от положения точки ее приложения. Поэтому во вращательном движении вместо силы вводится понятие момента силы М. Вектор М определяется векторным произведением M = [ R T 2] и является моментом силы T 2 относительно точки 0, из которой проводится радиус-вектор R точки приложения силы. Вращательному движению крестовины препятствует момент силы трения в подшипниках M тр. Проекции векторов M и M тр на ось вращения, проходящую через точку 0, называются моментами соответствующих сил относительно этой оси. Если радиус-вектор R совпадает с радиусом шкива 4, то момент силы Т 2 относительно оси вращения М = RT 2. Поскольку момент силы относительно оси вращения - величина алгебраическая, то М и М тр имеют противоположные знаки. Если при поступательном движении мерой инертности тела является его масса, то при вращательном движении инертность тела зависит от распределения массы относительно оси вращения, и мерой инертности является момент инерции тела J. В общем случае момент инерции тела относительно оси вращения J = где m i - масса i -ой частицы тела (тело разбито на n частиц); r i - расстояние от i -ой частицы до оси вращения. В случае маятника Обербека
J = J к + J п, (2)
где J к - момент инерции крестовины без привесок 3 (рис.1.3.1); J п - суммарный момент инерции привесок. В соответствии с теоремой Штейнера J п можно представить как
J п = 4 m 0 (
где m 0 - масса привески; d и l -диаметр и высота привески; r - расстояние от оси вращения до центра масс привесок. Изменяя положение привесок на стержнях крестовины, можно менять момент инерции J маятника. Для описания поступательного движения груза 8 можно применить второй закон Ньютона (основной закон динамики поступательного движения): m a = m g + T, (4)
а для описания вращательного движения крестовины маятника - основной закон динамики вращательного движения:
(J к + J п) e = M + M тр, (5)
где e - угловое ускорение крестовины маятника. Если пренебречь массой нити 5, моментом инерции блока 6 и силами трения в нем, то силы реакции нити Т 1 и Т 2 равны по абсолютной величине: Т 1 = Т 2 = Т. С учетом этих упрощений запишем уравнение (4) в проекциях на вертикальную ось, а уравнение (5) в проекциях на ось вращения: ma = mg - T, (6) (J к + J п) e = TR - M тр.
Учитывая, что ускорение груза а равно линейному ускорению точек на поверхности шкива, которое связано с угловым ускорением зависимостью a = e R, (7)
и исключая из системы (6) силу реакции Т, получим
e =
Из этого выражения видно, во-первых, что угловое ускорение не зависит от времени (ни одна из величин, входящих в правую часть, не меняется во время движения маятника), что доказывает равноускоренный характер вращения крестовины. Во-вторых, видно, что изменить угловое ускорение можно либо меняя момент инерции привесок J п, либо меняя массу груза m. В том, что вращение равноускоренное, можно убедиться в ходе выполнения лабораторной работы N 1.2 “Изучение кинематики вращательного движения”. Задачей данной лабораторной работы является экспериментальная проверка зависимости углового ускорения e крестовины от момента инерции привесок J п и массы груза m. Зависимости e (J п) и e (m), как следует из выражения (8), нелинейные. Поэтому для удобства экспериментальной проверки их следует линеаризовать (см.Приложение), т.е. выявить такие новые переменные, зависимость между которыми была бы линейной. Используя уравнения кинематики, можно показать, что e =
где h - путь, проходимый грузом 8 за время t. Подставив (9) в (8), получим следующую зависимость времени падения груза от момента инерции привесок: t 2 = b 1 + k 1 J п, (10) где b 1 = 2 h k 1 =
Для облегчения линеаризации зависимости e (m) упростим выражение (8), принимая во внимание следующее обстоятельство. По мере удаления привесок от оси вращения их момент инерции J п возрастает, что обусловливает увеличение доли составляющей J п + J к в знаменателе выражение (8) и, соответственно, уменьшение доли составляющей mR 2. При удалении привесок на расстояние r
где b 2 = - k 2 =
Из (10) следует, что квадрат времени падения груза должен линейно зависеть от момента инерции привесок при постоянстве остальных параметров. Из (13) следует, что величина, обратная квадрату времени падения груза, должна линейно зависеть от массы груза при постоянстве остальных параметров. Если графики экспериментальных зависимостей t 2 = f 1(J п) и 1/ t 2 = f 2(m) окажутся прямыми линиями в пределах погрешности измерений, то это будет означать, что зависимость (8) подтверждена экспериментально, а следовательно, справедливы основные законы динамики поступательного и вращательного движения (4) и (5), взятые за основу при выводе выражения (8). При этом свободный член b 1 зависимости (10) может быть определен как величина отрезка, отсекаемого графиком t 2 = f 1(J п) на оси t 2, а угловой коэффициент k 1 - как отношение D(t 2)/D J п, где D J п - произвольный отрезок на оси J п(приращение аргумента), D(t 2) - соответствующее приращение функции (см. Приложение). Аналогично можно определить коэффициенты b 2 и k 2 зависимости (13). Используя выражение (11), (12) и величины коэффициентов b 1, k 1 или выражение (14), (15) и величины коэффициентов b 2, k 2, можно определить такие параметры маятника Обербека, как момент инерции J к крестовины без привесок и момент силы трения M тр.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Включить в сеть шнур питания экспериментальной установки. 2. Нажать на кнопку “СЕТЬ”, расположенную на лицевой панели миллисекундомера, при этом должны загореться лампочка фотодатчика и цифровые индикаторы миллисекундомера, сработать электромагнитный фрикцион и зафиксировать крестовину. 3. Для снятия первой точки экспериментальной зависимости t 2 = f 1(J п) установить привески симметрично на минимальное расстояние r от оси вращения и зафиксировать их винтами. 4. Нажав на кнопку “ПУСК” на миллисекундомере и вращая крестовину против часовой стрелки, перевести груз в положение, соответствующее выбранному вами и постоянному в дальнейших измерениях пути h, проходимому грузом. Кнопку “ПУСК” отпустить. 5. Нажать на кнопку “СБРОС” и убедиться, что на индикаторах установились нули. 6. Нажать кнопку “ПУСК” и удерживать ее в нажатом положении до момента пересечения падающим грузом оптической оси фотодатчика. 7. Произвести отсчет времени опускания груза t по миллисекундомеру. Результаты измерений r и t занести в табл.1.3.1. 8. Повторить измерения по п.п.4-7 не менее пяти раз. 9. Произвести измерения по п.п.4-8 для других (не менее пяти) положений привесок на стержнях крестовины маятника Обербека. Все привески при этом должны быть расположены симметрично относительно оси вращения. Последнее положение привесок должно быть на самом конце стержней. Обратите внимание на то, что необходимо измерить и занести в табл.1.3.1 (в колонку “Примечание”) значения массы одной привески m 0, диаметра d и высоты l привески, высоты падения груза h, массы груза m и радиуса шкива R. 10. Для снятия экспериментальной зависимости 1/ t 2 = f 2(m) установить привески на расстояние r 11. Произвести измерения по п.п.4-8 времени опускания груза для различных значений его массы (не менее пяти). Результаты измерений m, t и r занести в табл.1.3.2. 12. Определить косвенно измеряемые величины экспериментальной зависимости t 2 = f 1(J п). Для этого по формуле (3) рассчитать моменты инерции I п привесок для измеренных значений r. Затем рассчитать t 2 для всех значений t и средние арифметические значения t 2, соответствующие каждому J п. Все значения J пи t 2 занести в табл.1.3.1. 13. Рассчитать погрешности величины t 2 для первой и последней экспериментальных точек. Погрешности остальных экспериментальных точек можно выбрать промежуточными между погрешностями крайних. 14. Определить значения косвенно измеряемой величины 1/ t 2 экспериментальной зависимости 1/ t 2 = f 2(m). Для этого рассчитать 1/ t 2 для всех значений t и средние арифметические значения 1/ t 2, соответствующие каждому значению m. Все значения 1/ t 2 занести в табл.1.3.2. 15. Рассчитать погрешности величины 1/ t 2 для первой и последней экспериментальных точек. Погрешности остальных экспериментальных точек можно выбрать промежуточными между погрешностями крайних. 16. Построить графики зависимостей t 2 = f 1(J п) и 1/ t 2 = f 2(m). Убедиться, что графики представляют собой прямые линии, проходящие через все доверительные интервалы. 17. Используя график зависимости t 2 = f 1(J п) или 1/ t 2 = f 2 Дата добавления: 2014-10-29; просмотров: 6721. Нарушение авторских прав; Мы поможем в написании вашей работы! Экспертная оценка как метод психологического исследования Экспертная оценка – диагностический метод измерения, с помощью которого качественные особенности психических явлений получают свое числовое выражение в форме количественных оценок...
Образование соседних чисел Фрагмент:
Программная задача: показать образование числа 4 и числа 3 друг из друга...
|

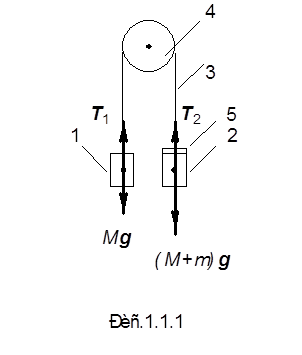
 . (4)
. (4) .
. , (7)
, (7) , (8)
, (8)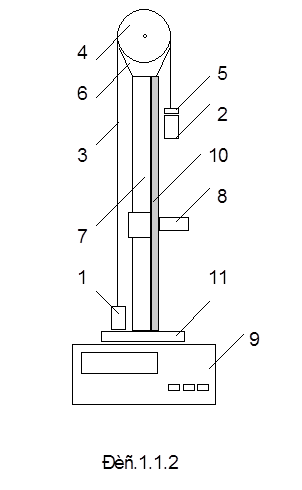
 3%, что позволяет в данной работе вместо выражения (4) использовать упрощенное выражение (8). Блок 4 с узлом подшипников крепится к верхнему кронштейну 6 стойки 7. Кроме того, на верхнем кронштейне находится электромагнит, который при подаче на него напряжения с помощью фрикциона удерживает систему с грузами в неподвижном состоянии.
3%, что позволяет в данной работе вместо выражения (4) использовать упрощенное выражение (8). Блок 4 с узлом подшипников крепится к верхнему кронштейну 6 стойки 7. Кроме того, на верхнем кронштейне находится электромагнит, который при подаче на него напряжения с помощью фрикциона удерживает систему с грузами в неподвижном состоянии.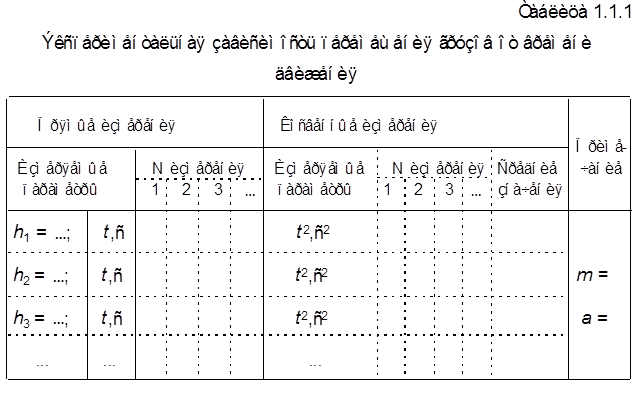
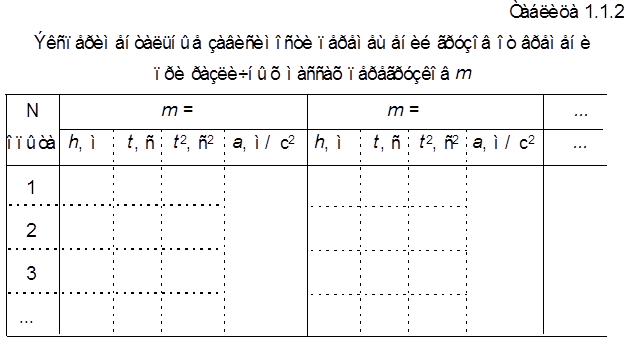

 . (4)
. (4) , (6)
, (6) , (9)
, (9)
 .(10)
.(10)
 0, то как будут выглядеть графики зависимостей j = f 1(t) и j = f 2(t 2)?
0, то как будут выглядеть графики зависимостей j = f 1(t) и j = f 2(t 2)?
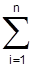 m i r i2, (1)
m i r i2, (1) +
+ 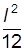 ) + 4 m 0 r 2, (3)
) + 4 m 0 r 2, (3) . (8)
. (8)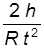 , (9)
, (9) , (11)
, (11) . (12)
. (12) 15 см и максимальном для данного маятника значении m доля составляющей mR 2 не превышает 0, 5% для R = 21 мм и 2% для R = 42 мм, что позволяет пренебречь этой составляющей при указанных условиях (r
15 см и максимальном для данного маятника значении m доля составляющей mR 2 не превышает 0, 5% для R = 21 мм и 2% для R = 42 мм, что позволяет пренебречь этой составляющей при указанных условиях (r 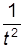 = b 2 + k 2 m, (13)
= b 2 + k 2 m, (13)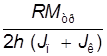 , (14)
, (14) . (15)
. (15)


