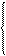Однофакторна модель Брауна
n, t – кількість років спостереження; Рі - величина показника у відповідному році спостереження;
Питома вага показника відповідного року розраховується по декількох формулам:
Аі - питома вага показника відповідного року
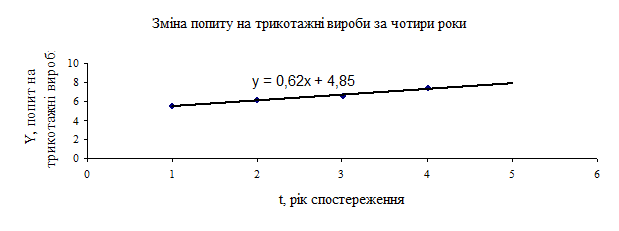
Відносно даної задачі А4 = 2/(4+1) = 0, 4 Аt-1 = At * (1 - At) Відносно даної задачі А3 = A4 * (1 – A4) = 0, 4 * (1 – 0, 4) = 0, 4*0, 6 =0, 24 Аt-2 = At * (1 - At)2 Відносно даної задачі А2 = A4 * (1 – A4)2 = 0, 4 * (1 – 0, 4)2 = 0, 4*0, 36 =0, 144 Аt-3 = At * (1 - At)3 Відносно даної задачі А1 = A4 * (1 – A4)3 = 0, 4 * (1 – 0, 4)3 = 0, 4*0, 216 =0, 086 Аt-4 = At * (1 - At)4 Відносно даної задачі А0 = A4 * (1 – A4)4 = 0, 4 * (1 – 0, 4)4 = 0, 4*0, 13 =0, 052 В загальному вигляді Аі розраховується по формулі: ∑ Аі = А4+ А3+ А2+ А1+ А0 = 0, 4+0, 24+0, 144+0, 086+0, 052 = 0, 922
Р5=0, 434*7, 1+0, 26*6, 6+0, 156*6, 1+0, 093*5, 5+0, 056*0 = 6, 261 шт. трикотажних виробів на 1 люд Загальний попит на трикотажні вироби в регіоні = 6, 261*125000 = 782625 шт.
2.Модель апроксимації даних. Дана модель розраховується рівнянням прямої лінії у = а0 + а1*t де t – рік спостереження. Коефіцієнти
∑ Y*t = а0 *∑ t + а1*∑ t2
Для розв’язання даної системи рівнянь будуємо допоміжну таблицю: Таблиця 9 Допоміжна таблиця
25.6 = а0 *4 + а1*10 67.1 = а0 *10 + а1*30
Розв'язавши системи двох рівнянь з двома невідомими отримали: а0 = 4, 85 а1 = 0, 62 Тоді рівняння прямої лінії даної задачі
у = 4, 85 + 0, 62*t Наносимо дану пряму лінію на графік (рис. 1) Графічне зображення зміни попиту на протязі чотирьох років спостереження на рисунку 1
Рис.1 Зміна попиту на протязі чотирьох років спостереження
Для визначення загального прогнозу попиту трикотажних виробів у п'ятому році спостереження в рівняння прямої лінії підставляємо t = 5 Y5 = 4, 85 + 0, 62*5 = 7, 95 шт. трикотажних виробів на 1 люд Загальний попит на трикотажні вироби в регіоні = 7, 95*125000 = 993750 шт.
Висновок: загальний прогноз попиту трикотажних виробів в регіоні в п'ятому році спостереження за наступними методами: - за методом однофакторної моделі Брауна попит складає - 782625 шт. - за методом апроксимації даних попит складає – 993750 шт.
|

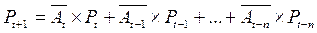

 - приведена питома вага показника відповідного року.
- приведена питома вага показника відповідного року. ;
;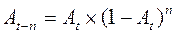
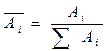
 А4 = А4/∑ Аі = 0, 4/0, 922 = 0, 434
А4 = А4/∑ Аі = 0, 4/0, 922 = 0, 434 А2 = А2/∑ Аі = 0, 144/0, 922 = 0, 156
А2 = А2/∑ Аі = 0, 144/0, 922 = 0, 156 А1 = А1/∑ Аі = 0, 086/0, 922 = 0, 093
А1 = А1/∑ Аі = 0, 086/0, 922 = 0, 093 А0 = А0/∑ Аі = 0, 052/0, 922 = 0, 056
А0 = А0/∑ Аі = 0, 052/0, 922 = 0, 056 - коефіцієнти лінії тренду;
- коефіцієнти лінії тренду; ∑ Y = а0 *n + а1*∑ t
∑ Y = а0 *n + а1*∑ t