Определение напряжений в плоских крышках и днищах
Под внутренним избыточным давлением Плоские крышки и днища широко распространены в машиностроении и их можно рассматривать как тонкие пластинки, у которых толщина меньше 1/5 наименьшего размера основания. За наименьший размер основания у упругих пластинок принимают диаметр, у прямоугольных – меньшую сторону, у эллиптических – меньшую ось эллипса и т. д. Под действием внешних нагрузок в плоских крышках и днищах одновременно могут возникать как напряжение изгиба, так и напряжения растяжения или сжатия, которые еще называются мембранными напряжениями. В зависимости от характера напряженного состояния и величины прогиба тонкие пластинки могут подразделяться на жесткие, гибкие и мембранные. Для жестких пластинок характерно преобладание изгибных напряжений, а их прогиб не превышает 1/4 толщины пластинки. У гибких пластинок изгибные и мембранные напряжения сравнимы, а прогиб изменяется в пределах от 1/4 толщины до 5 толщин. И, соответственно, у мембран преобладают мембранные напряжения, и прогиб превышает 5 толщин пластинки. При расчетах плоские днища, крышки, фланцы и т.д. рассматриваются как жесткие пластинки. Форма днища бывает эллиптической, конической, полушаровой и плоской. ЦЕЛЬ РАБОТЫ Теоретически и экспериментально определить напряжения, действующие на поверхности плоской крышки и плоского днища, для заданных значений внутреннего давления, сравнить экспериментальные значения с расчетными и определить процент отклонения. СОДЕРЖАНИЕ РАБОТЫ Расчет напряжений вплоских круглых крышках или днищах ведется согласно теории тонких пластинок, по которой общие уравнения круглых пластинок, нагруженных симметрично, записываются в дифференциальной форме:
Уравнения изгибающихся моментов записывается в виде:
где Mr – радиальный момент, отнесенный к единице длины; Mt – кольцевой момент, отнесенный к единице длины, φ - угол поворота нормали к срединной поверхности; W – прогиб пластинки на некотором радиусе окружности; r – текущий радиус; Уравнения (2.1) и (2.2) называются уравнениями углов поворота нормалей и прогибов пластинки в дифференциальной форме. Так как способ закрепления крышки или днища по краям (рис. 2.1) влияет на величину и характер распределения этих напряжений, то конструктивную схему можно свести к шарнирной (рис. 2.2) или жестко защемленной (рис. 2.3).
Рис. 2.1.
Рис. 2.2. Рис. 2.3. В действительности же будет иметь место промежуточный случай, тo есть упругая заделка края. Для определения перерезающей силы, независимо от способа заделки края крышки или днища, уравнение равновесия центральной частикрышки радиуса r (рис. 2.4) запишется в виде:
Откуда:
Рис. 2.4. Подставив значение Q в уравнение (2.1) и дважды проинтегрировав его, получим:
где С1 и С2 – постоянные интегрирования. Постоянная интегрирования С2 определяется из условия, что в центре крышки или днища при
Постоянная С1 интегрирования определяется из второго граничного условия при Для жесткозащемленного случая когда при
Для шарнирного закрепления при
Подставим в уравнение (2.10) значение угла поворота нормалей к срединной поверхности
С учетом выражения (2.11) уравнение (2.8) для шарнирного закрепления перепишется:
Подставив в уравнения (2.3), (2.4) значения для жесткого защемления:
для шарнирной заделки:
Нормальные радиальные и кольцевые напряжения, действующие на поверхности плоской крышки или днища, найдутся в общем виде как
Тогда, в зависимости от способа закрепления крышки или днища по контуру, выражения (2.15), (2.16) с учетом (2.13), (2.14) перепишутся в виде: для жесткого защемления:
для шарнирной заделки:
3 ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ И МЕТОДИКАПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА
Рис. 3.1. Расстояние по радиусу от центра крышки (днища) до исследуемой точки r1, r2, r3, r4 замерить на установке и занести в таблицу 4.2. Переключая тумблер 13 из положения 0 в положение 9 снять показания тензостанции при ненагруженных тензодатчиках 5 с помощью электронно-цифрового вольтметра 7 изанести эти показания таблицу 4.2. Закрыть вентиль 14. Создать давление в аппарате, снять показания на манометре 4 до заданного значения давления; но не свыше 3 МПа. Снять показания тензостанции с помощью электронного цифрового вольтметра 7, переключая тумблер 13 из положения 9 в положение 0. Открыть вентиль 14, сбросить давление в аппарате 1 и выдержать 5 минут. Повторить испытание и, если показания не совпадают, подрегулировать каналы. Переключая тумблер 13, нагружать тарировочную балку 10 нагрузкой, величина которой должна соответствовать показаниям электронно-цифрового вольтметра 7 при нагруженных датчиках. Определить с помощью индикатора 8 величину прогиба тарировочной балки 10.
|

 (2.1)
(2.1) (2.2)
(2.2) (2.3)
(2.3)
 (2.4)
(2.4) - цилиндрическая жесткость пластины; Е – модуль упругости первого рода;
- цилиндрическая жесткость пластины; Е – модуль упругости первого рода;  - толщина пластинки;
- толщина пластинки;  - коэффициент Пуассона; Q – перерезывающая сила.
- коэффициент Пуассона; Q – перерезывающая сила.

 . (2.5)
. (2.5) . (2.6)
. (2.6)
 (2.7)
(2.7) , а это возможно только в том случае, когда С2=0 в уравнении (2.7). Следовательно, уравнение (2.7) можно представить в виде:
, а это возможно только в том случае, когда С2=0 в уравнении (2.7). Следовательно, уравнение (2.7) можно представить в виде: (2.8)
(2.8) и зависит от способа закрепления крышки по контуру.
и зависит от способа закрепления крышки по контуру. , из уравнения (2.8) имеем, что
, из уравнения (2.8) имеем, что  . Тогда уравнение (2.8) перепишется:
. Тогда уравнение (2.8) перепишется: (2.9)
(2.9) и из уравнения (2.3) имеем:
и из уравнения (2.3) имеем: (2.10)
(2.10) из уравнения (2.8) и производную
из уравнения (2.8) и производную  , а затем, решим его относительно С1.
, а затем, решим его относительно С1. (2.11)
(2.11) (2.12)
(2.12) (2.13)
(2.13) ,
, (2.14)
(2.14) .
. (2.15)
(2.15) (2.16)
(2.16) (2.17)
(2.17)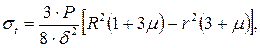 (2.18)
(2.18) (2.19)
(2.19) (2.20)
(2.20) Схема экспериментальной установки представлена на рисунке 3.1. Основным элементом является тонкостенный цилиндрический аппарат 1, снабженный плоской разъемной крышкой 2 и плоским приварным днищем 3. Рабочее давление в аппарате 1, заполненным касторовым маслом, создается грузопоршневым манометром 4 (МП-600). Под действием давления в материале плоской крышки и плоского днища возникают деформации, которые воспринимаются тензодатчиками 5, наклеенными на наружной поверхности. Сигнал от тензодатчиков поступает на тензостанцию 6 («Топаз 3-4-01») и регистрируется электронным цифровым вольтметром 7 (В7-20). После снятия рабочего давления в аппарате 1 с помощью индикатора часового типа 8, установленного на тарировочном устройстве 9, по показаниям электронного цифрового вольтметра 7 определяется прогиб балки 10, на которой наклеены компенсационные датчики 11 и 12.
Схема экспериментальной установки представлена на рисунке 3.1. Основным элементом является тонкостенный цилиндрический аппарат 1, снабженный плоской разъемной крышкой 2 и плоским приварным днищем 3. Рабочее давление в аппарате 1, заполненным касторовым маслом, создается грузопоршневым манометром 4 (МП-600). Под действием давления в материале плоской крышки и плоского днища возникают деформации, которые воспринимаются тензодатчиками 5, наклеенными на наружной поверхности. Сигнал от тензодатчиков поступает на тензостанцию 6 («Топаз 3-4-01») и регистрируется электронным цифровым вольтметром 7 (В7-20). После снятия рабочего давления в аппарате 1 с помощью индикатора часового типа 8, установленного на тарировочном устройстве 9, по показаниям электронного цифрового вольтметра 7 определяется прогиб балки 10, на которой наклеены компенсационные датчики 11 и 12.


