Погрешность определения площадей с использованием палетки
По координатам точек построенного замкнутого теодолитного хода вычисляется площадь полигона по формулам:
т. е. площадь полигона S равняется половине суммы произведений ординат каждой точки на разность абсцисс предыдущей и последующей точек или половине суммы произведений абсциссы каждой точки на разность ординат последующей и предыдущей точек. Вычерчиваются на кальке квадратные сетки со стороной квадрата, равной 2 см, 1 см и 0, 5 см (палетки). Палетка накладывается на полигон и определяется его площадь. Затем палетка смещается и определяется эта же площадь второй раз. Из двух определений вычисляется среднее значение площади, если расхождение между этими определениями не превышает 1: 100 определяемой площади Средние значения площадей вычисляются по палеткам с разными квадратами. Погрешность определения площади палеткой находится по формуле
где П - относительная погрешность определения площади палеткой; S - площадь полигона, вычисленная по аналитической формуле; Sср - площадь полигона, полученная с использованием палетки. Полученные данные анализируются и формулируются выводы.
Погрешность определения площадей с использованием планиметра
Перед измерением площади полигона вычисляется цена деления планиметра путем тройного обвода известной площади S по формуле
где с - цена деления планиметра; S - известная площадь; D О - средняя разность отсчетов по планиметру,
Пример измерений и вычислений приводится в таблице 2.5. Таблица 2.5. – Определение цены деления планиметра
Полигон обводится дважды планиметром и вычисляется площадь полигона:
где с – цена деления планиметра; D О – средняя разность отсчетов по планиметру при двух обводах площади. Вычисляется погрешность определения площади планиметром по формуле
Данные измерений и вычислений анализируются и формулируются выводы.
|

 ,
, ,
, ,
, ,
,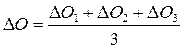 , вычисляется, если разности отсчетов D О 1, D О 2 и D О 3 отличаются не более чем на 2 единицы при площади до 200 делений, 3 единицы при площади 200 – 2000 делений и 4 единицы при площади свыше 2000 делений.
, вычисляется, если разности отсчетов D О 1, D О 2 и D О 3 отличаются не более чем на 2 единицы при площади до 200 делений, 3 единицы при площади 200 – 2000 делений и 4 единицы при площади свыше 2000 делений. ,
, . (2.1)
. (2.1)


