Вычисление координат точек теодолитного хода
Вычисление координат точек теодолитного хода ведется в следующей последовательности (см. таблицу 2.4). Таблица 2.4 – Пример на вычисление координат точек теодолитного хода
1. В графу 1 заносятся номера точек теодолитного хода I, II, III, IV, V, I. 2. В графу 2 вписываются значения горизонтальных углов против соответствующих номеров точек. Величины этих углов берут из журнала теодолитной съемки (см. таблицу 2.1, графы 7 и 8). Всего должно быть пять значений углов. 3. Подсчитывают сумму измеренных углов, т. е. 4. Вычисляют теоретическую сумму внутренних углов полигона:
где n - число углов многоугольника. 5. Определяют фактическую угловую невязку:
6. Подсчитывают допустимую угловую невязку:
где t = 30" - точность прибора; n - число измеренных углов. 7. Убедившись, что допустимая угловая невязка больше фактической невязки, приступают к увязыванию углов. Для этого надо к каждому измеренному углу прибавить поправку, равную угловой невязке с обратным знаком, деленной на число углов. Однако в целях упрощения расчета рекомендуется распределить угловую невязку таким образом, чтобы исправленные углы не имели секунд, т. е. содержали бы только величины градусов и минут. Поправки выписываются красными чернилами над секундами в графе 2. Сумма исправленных углов в графе 3 должна равняться теоретической сумме углов пятиугольника. 8. Увязав углы, приступают к вычислению дирекционных углов сторон полигона II-III, III-IV, IV-V, V-I (графа 4 таблицы 2.4): где bII, bIII,... - исправленные горизонтальные углы полигона (см. графу 3, таблицы 2.4). Если дирекционный угол по величине получается больше 360º, то из этого угла необходимо вычесть 360°. 9. Контролем правильности вычисления дирекционных углов сторон теодолитного хода служит равенство исходного дирекционного угла aI-II и угла aI-II, полученного по формуле 10. Производят вычисление румбов сторон полигона. Если сторона полигона имеет дирекционный угол, находящийся в первой четверти (от 0 до 90º), то величина румба равна величине дирекционного угла. Пример1. a = 75º 37´, то r = СВ: 75º 37´. Если дирекционный угол полигона находится во второй четверти (90 до 180º), то табличный угол равен 180º минус дирекционный угол. Пример 2. a = 128º 33´, то r =ЮВ: 51º 27´. Если сторона теодолитного хода имеет дирекционный угол в третьей четверти (от 180 до 270º), то румб стороны определяется как разность между значением дирекционного угла и 180º. Пример 3. a = 200º 15´, то r = ЮЗ: 20º 15´. И если дирекционный угол стороны полигона проходит через четвертую четверть (от 270 до 360º), то румб этой стороны вычисляется как разность между 360º и величиной дирекционного угла. Пример 4. a = 300º 20¢, то r = СЗ: 59º 40¢. 11. В графу 6 (см. таблицу 2.4) выписываются горизонтальные проложения длин линий, которые вычисляются как произведение среднего значения измеренной длины на косинус угла наклона линии. Пример. Среднее значение из двух измерений стороны I–II теодолитного хода (см. таблицу 2.1, графа 9) равняется (161, 63 + 161, 59): 2 = 161, 61 м Угол наклона линии I–II (см. таблицу 2.1, графа 10) 5°. Горизонтальное проложение линии I–II составит: 161, 61× cos5° = 161, 00 м. Все длины линий суммируются и получают периметр полигона P. 12. Вычисляются приращения координат DХ и DУ (см. графы 7 и 8 таблицы 2.4): DХ = ± d× cos r, DY = ± d× sin r, где d – горизонтальное положение линии хода; r – величина румба линии. Знак приращения устанавливается в зависимости от направления линии. Если линия направлена на северо-восток (первая четверть), то DХ и DY - положительные. Если линия имеет юго-восточное направление (вторая четверть), то DХ принимает отрицательное, а DY- положительное значение. Если линия проходит через третью четверть (юго-западное направление), то DХ и DY - отрицательные. Если линия направлена на северо-запад, то DХ принимает положительное значение, а DY - отрицательное значение. Пример. Дано d = 241, 00 м, r = ЮВ: 70°32'. Найти: DХ и DY. Так как направление юго-восточное, то DХ = – 241, 00 × cos 70°32' = – 80, 32 м, DY = + 241, 00 × sin 70°32' = +227, 22 м. Вычисление невязок по координатным осям: f x = å DХ, f У = å DY, где å DХ, å DY - суммы вычисленных приращений координат по осям Х и Y соответственно. 14. Вычисление общей невязки в периметре теодолитного хода:
15. Определение относительной погрешности теодолитного хода и сравнение ее с допустимой:
где Р - периметр полигона. Пример: fх = - 0, 32, fу = + 0, 28, Р = 1137, 70.
Следовательно, можно приступить к увязке приращений координат. Увязка производится путем введения поправок в вычисленные приращения координат. Поправки в приращение координат вводятся пропорционально длинам сторон хода со знаком, обратным невязке. Пример. fх = - 0, 32 м, d = 231, 29 м, Р = 1137, 70 м, DХ = 210, 31м. Вычислить исправленное приращение. Поправка в приращении координат q 1 = + 0, 32: 1137, 70 × 231, 29 = + 0, 06 м. Поправка + 0, 06 м подписывается красными чернилами над вычисленным приращением. Исправленное приращение DХ = 210, 31 + 0, 06 м = 210, 37 (см. таблицу 2.4, графы 7 и 9). Следует заметить, что сумма поправок должна равняться невязке с обратным знаком, т.е. å q i = - f x. В графы 9 и 10 таблицы 2.4 записываются исправленные приращения, которые численно равны алгебраической сумме вычисленного превышения плюс поправка. Контролем правильности выполненных действий по увязке координат являются суммы исправленных приращений отдельно по осям Х и Y, т.е. å DХ = 0 и å DY = 0. В задании должны быть вычислены и увязаны десять приращений координат. 16. Вычисление координат точек теодолитного хода. Координаты точки I принимаются согласно шифру. Координаты последующих точек вычисляются по формулам: Х n + 1 = Х n + DХ, Y n + 1 = Y n + DY, где Х n и Y n - абсцисса и ордината предыдущей точки; DХ и DY - приращения координат по оси Х и Y между предыдущей и последующей точками соответственно. Контролем правильности вычисления координат точек является получение координат первой точки:
Пример вычисления координат теодолитного хода приводится в таблице 2.4.
|

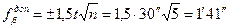

 <
< 
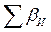 , и записывают ее под чертой в графе 2 таблицы 2.4.).
, и записывают ее под чертой в графе 2 таблицы 2.4.). ,
, .
. ,
, ,
, ,
,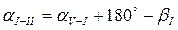 .
. .
. ,
,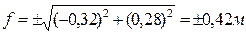 ,
,  <
<  .
. ,
,  .
.


