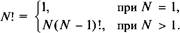Процедуры и функции. Рекурсия

Упражнение № 9. Процедуры

Пример 25. Составить программу, которая будет находить а^п, то есть п-ю сте­пень числа а, где а и п — это целые числа и п > 0, вводимые с клавиатуры.

Решение. Составим процедуру, которая вычисляет степень целого числа.

Ргодгат Ехатр1е_25;

Уаг а, п: 1п1: едег; з: Ьопд1п" Ь;

Ргосейиге Оедгее(х, у: 1п1: едег; Уаг з" Ь: Ьопдл-п!:);

Уаг 1: 1п-Ьедег;

Вед±п

з" Ь: =1;

Гог 1: =1 То у Во 5" Ь: =5" Ь*х;

Епс1; Вед±п

Мгл_1: е1п (' введите два числа'); {ввод значений} КеасИп (а, п);

Бедгее (а, п, з); {обращение к процедуре} Мгл_1: е1п (' Результат ', з); {вывод значения а^п} КеасИп; Епс1.

Пример 26. Даны два целых числа. Поменять местами их значения. Решение. Менять местами значения двух чисел можно двумя способами — через промежуточную переменную или без нее. Напишем процедуру, воспользовавшись первым способом.

Ргодгат Ехатр1е__2 6; Уаг а, Ь: 1п-Ьедег;

Ргосейиге Змар (Уаг х, у: 1п1: едег);

Уаг г: 1п" Ьедег;

Вед±п

2: =х; х: =у; у: =г; Епс1; Ведхп

Мгл_1: е1п (' введите два числа'); {ввод значений} КеасИп (а, Ь);

5мар(а, Ь) {обращение к процедуре} Мгл_1: е1п (' а= ', а, ' Ъ=', Ъ); {вывод новых значений} КеасИп; Епс1.

Задания для самостоятельной работы

1. Используя процедуру из примера 25, вычислить значение выражения

у = а_хх^А + а₂х³ + а₃х² + а₄х + а₅,

где коэффициенты а_и а₂, а₃, а₄, а₅ их — это числа, вводимые с клавиатуры.

2. Используя процедуру из примера 26, упорядочить значения трех переменных а, Ь и с в порядке их возрастания.

3. Даны координаты трех вершин треугольника. Найти длины всех его сторон.

4. Дано натуральное число. Найти все его делители. Подсчитать их число.

5. Даны два натуральных числа. Определить, является ли первое число перевер­тышем второго?

6. Даны координаты трех вершин треугольника АБС и даны координаты четвер­той точки В. Определить, является ли эта точка внутренней точкой треугольника.

Упражнение № 10. Функции

Пример 27. Составить программу, подсчитывающую число сочетаний без повто­рения из N элементов по К элементов.

Решение. Число сочетаний без повторения считается по формуле

С^к = ^{п1 п} к\(п-к)\'

Обозначим п, к — переменные для хранения введенных чисел; С — переменная для хранения результата.

Чтобы подсчитать число сочетаний без повторения, необходимо вычислить п\, (п - к)!, к\.

Опишем функцию, вычисляющую факториал числа п (п! = 1-2 •... п).

Ргодгат Ехатр1е_27;

У& г п, к: 1п-Ьедег;

а1, а2, аЗ, с: Ьопдл_п1:;

ЕЧдпсЫоп ^ас1: ог1а1 (п: 1п-Ьедег): Ъопдл.п-Ь;

Уаг 1: 1п-Ьедег;

гег: Ьопдл_п1:;

Вед±п

гег: =1;

Гог ±: =1 То п Во гег: =ге2*л_; ^ас1: ог1а1: =гег; Еп< 1; Вед±п

ДОгИ: е1п (¹ Введите пик для подсчета числа сочетаний из п по к '); Кеас11п (п, к);

а1: = ^ас-Ьог1а1 (п); { вычисление п! } а2: = ^ас-Ьог1а1 (к); {вычисление к! } аЗ: = ^ас-Ьог1а1 (п-к); {вычисление (п-к)! } с: =а1 ^^V (а2*аЗ); {результат} ДОг11: е1п (с); Кеас11п; Еп< 1.

Пример 28. Написать функцию, подсчитывающую количество цифр числа. Ис­пользуя ее, определить, в каком из двух данных чисел больше цифр.

Решение. Для решения задачи вспомним, как подсчитать количество цифр. Для этого можно выделять последнюю цифру до тех пор, пока число не станет равным нулю. При этом каждый раз надо увеличивать счетчик на 1 (начальное значение счетчика — 0). Ргодгат Ехатр1е_28; Уаг п1, п2: 1юпдл.п-Ь;

к1, к2: Ву^е; РипсЪ±оп Оиап^л-^у (х: 1юпдл.пЪ): Ву^е; Уаг к: Ву^е; Вед±п к: =0;

ДОЬНе х < > 0 Во Вед±п

1пс(к); х: =х ^^V 10; Еп< 1;

Оиап'Ы'Ьу: =к; Епй; Вед±п

^г1" Ье1п (' Введите два числа'); {ввод чисел} Кеас11п (п1, п2);

к1: = ОиапЪл-Ъу (п1); {количество цифр первого числа} к2: = Оиап^-Ьу (п2); {количество цифр второго числа} {Сравнение количества цифр в числах}

к1=к2 ТЬеп ДОгл_{: е1п (¹ Одинаковое количество цифр¹) Е1зе I^ к1> к2 ТЬеп ^г11: е1п(¹В первом числе цифр больше¹) Е1зе Мг1{: е1п (¹ Во втором числе цифр больше¹); Кеас11п;

Епс1.

Задания для самостоятельной работы

1. Найти сумму цифр числа.

2. Найти первую цифру числа.

3. Найти количество делителей числа.

4. Найти числа из промежутка от А до Д у которых больше всего делителей.

5. Найти сумму всех делителей числа.

6. Определить, является ли число совершенным, то есть равно ли оно сумме своцх делителей, кроме самого себя (используя преобразованную функцию из пре­дыдущего примера).

7. Определить, является ли число простым.

8. Среди чисел из интервала от А до В найти все простые.

9. Составить программу, проверяющую, является ли число палиндромом (на­пример, число 12721 — палиндром).

10. Определить, является ли число автоморфным, то есть квадрат этого числа заканчивается этим же числом, например число 6, так как его квадрат 36 заканчи­вается на 6 или число 25 — его квадрат 625.

11. Используя функцию из предыдущей задачи, найти все автоморфные числа из промежутка от А до В.

Примечание. Задачи 8 и 11 можно модифицировать — найти N первых таких чисел или найти первые N таких чисел, начиная с числа М.

12. Составить программу нахождения наибольшего общего делителя нескольких чисел, используя функцию нахождения НОД двух чисел.

13. Составить программу, вычисляющую наименьшее общее кратное четырех заданных с клавиатуры чисел (использовать функцию из предыдущего примера).

14. Дано четыре числа. Вывести на экран наибольшую из первых цифр заданных чисел. Например, если а = 25, Ь — 730, с = 127, й = 1995, то должна напечататься цифра 7.

15. Дано натуральное число п. Выяснить, имеются ли среди чисел п, п + 1,..., 2п близнецы, т.е. простые числа, разность между которыми равна двум.

Упражнение № 11. Примеры рекурсивного программирования

Пример 29. Вычисление факториала натурального числа.

Решение. Для того чтобы вычислить ТУ!, надо знать значение (#-1)! и умножить его на N. при этом 1! =1. В общем виде это можно записать так:

 

РипсЪ±оп ^асЬог1а1 (п: 1п1: едег): Ъопд1п-Ь;

Вед±п

I^ п=1 ТЪеп ^асЬог1а1: =1

Е1зе ^асЬог1а1: =п*^асЬог1а1(п-1);

Епс1;

Найдем 5!. Как же будет вычисляться факториал этого числа? Первый вызов этой функции будет из основной программы (Например, а: = ^асЪог: 1а1 (5), где переменной а присваиваем значение 5!).

Так как то пойдем по ветке Е1зе и функции Еас1: ог1а1 присваиваем значение п*РасЪог1а1 (п-1), то есть надо умножить 5 на значение функции ГасЬог1а1 (4). Поэтому обращаемся второй раз к этой же функции, но переда­ем ее новое значение параметра — 4. Так делаем до тех пор, пока не передадим значение, равное 1. Тогда N = 1, а поэтому значение функции РасЪог1а1: =1. Таким образом, N = 1 — это условие, по которому процесс входа в следующую рекурсию заканчивается. Идет возвращение в точку вызова и подстановка в оператор присвоения значения вычисленной функции. То есть возвращаемся в предыдущую функцию для п=2: РасЪог1а1: =п*Рас1: ог1а1 (п-1), значит, Гас1: ог1а1: =2*1, следовательно, РасЪог1а1 (2) =2. И возвращаемся дальше. Таким образом, получаем значение РасЪог1а1 (5) =120, это значение и при­своим переменной а.

Пример 30. Перевод натурального числа из десятичной системы счисления в двоичную.

Решение. Для решения этой задачи рассмотрим сначала, как перевести число из десятичной системы счисления в двоичную. Пусть есть число 39, которое и надо представить в двоичной системе. Для этого разделим его на 2, получим целую часть и остаток от деления. Целую часть снова делим на 2 и получаем целую часть и остаток. Так делаем до тех пор, пока целую часть можно делить на 2 (то есть пока она не станет равной 1).

38 19

1 18 9

1 _8_ _4

1 4_______ 2

0 _2_ 1 0

Теперь, начиная с этой единицы, выписываем в обратном порядке все остатки от деления, это и будет запись числа 39 в двоичной системе счисления:

39, о= 100111₂.

Таким образом можно переводить любое натуральное число из десятичной си­стемы счисления в двоичную, а также и в другие системы (например, восьмерич­ную или шестеричную).

Опишем процедуру:

Ргосейиге Кес(п: 1п1: едег);

Вед1п

I^ п> 1 ТЪеп Кес (п 2);

ИгНе (п Мое! 2); Еп< 1;

Первая цифра (1) выводится на экран из последнего вызова, следующая цифра (0) из предпоследнего и так далее, последняя (1)— из первого. Таким образом, вывод очередной цифры происходит перед тем, как выйти из данной функции.

Задания для самостоятельной работы

1. Составить рекурсивную программу ввода с клавиатуры последовательности чисел (окончание ввода — 0) и вывода ее на экран в обратном порядке.

А(п, т) =

2. Составить программу вычисления значений функции Аккермана для неотри­цательных чисел пит, вводимых с клавиатуры.

т + 1, если п = 0,

А(п - 1, 1), если п Ф 0, т = 0,

А(п - 1, А(п, т - 1)), если п > 0, т > 0.

3. Найти сумму первых N членов арифметической (геометрической) прогрессии.

4. Найти первые N чисел Фибоначчи. Каждое число Фибоначчи равно сумме двух предыдущих чисел при условии, что первые два равны 1 (1, 1, 2, 3, 5, 8, 13, 21,...), поэтому в общем виде я-е число можно определить так:

_ А' ^если ^ = Ь я = 2,

[Ф(п -1) + Ф(п - 2), если п > 2.

5. Определить, является ли заданное натуральное число простым.

6. Для заданного натурального числа 7У> 1 определить единственное натураль­ное число а, для которого выполняется неравенство: 2^а~^х< М< 2^а.

Ш

7. Функция Р(п) определена для целых положительных чисел следующим образом:

1, если п - 1,

п

(Ну/), еслип > 2.

1/=2

Вычислить значения этой функции для п = 5, 6, 7,..., 20. Прорисовать вызовы (обратить внимание, что из одной функции может быть несколько вызовов этой же функции).

Файлы

Упражнение № 12. Файловый тип данных. Открытие файла.

Чтение и запись

Пример 31. Прочитаем файл целых чисел и выведем их на экран:

Аззхдп (Е1, ' а: 1П1:.с! а1: '); {связываем с внешним файлом} Кезе1: (Е1); {открываем его для чтения}

N01: ЕОЕ (Е1) Во {пока не достигнут конец файла Е1}

Вед±п

Кеас1(Е1, п); {считываем очередное число} ДОг1" Ье (п, ¹ '); {выводим его на экран} Еп< 1;

С1озе(Е1); {закрываем файл}

Пример 32. Создадим файл целых чисел с именем Оап1.с1а1, причем ни одно из чисел не равно 0.

Решение. Первоначально «свяжем» файловую переменную с конкретным вне­шним файлом при помощи процедуры Аззхдп. Откроем файл для записи — про­цедура Кемгл_-Ье. Конец ввода чисел— ввод числа ноль.

Ргодгат Ехатр1е_32; Уаг Е: Ел_1е 1п*: едег; п: 1п" Ьедег;

Вед±п

Азз1дп(Е, ¹ а: с! ап1.с1а" Ь ¹); {связываем с внешним файлом} Кемгл_" Ье (Е); {открываем его для записи} ДОгл_1: е1п (' конец ввода чисел - О¹); Кереа" Ь {пока не будет введен 0} ДОг1-Ье1п (' введите число'); Кеас11п(п); {ввод числа с клавиатуры}

{если введено число, отличное от О,

то дописываем его в данную строку файла Р1} п< > 0 ТЪеп Югл_{: е (Е, п); Ш-ЬИ п=0; {если ввели 0, то заканчиваем запись данного файла} С1озе(Е); {закрываем файл} Еп< 1.

Пример 33. В файле Оап1.с1а1 записаны целые числа (см. предыдущую задачу). Вы­числить сумму элементов и результат вместе с исходными данными записать в файл 0ап2.с1а1.

Ргодгат Ехатр1е_33;

Уаг Е1, Е2: ЕИе 01: 1п" Ьедег; {файловые переменные }

3, Ы: 1п" Ьедег; Вед±п

{с именем файла Е1 связывается внешний файл на дискете} А551дп(Е1, ' Бап1. с! а" Ь ¹); Кезе" Ь (Е1);

{открытие файла Е1 для чтения }

{с именем файла Е2 связывается внешний файл на дискете} А551дп(Е2, 'Бап2. с! а" Ь ');

Кемгл--Ье (Е2); {открытие файла Е2 для записи} 5: =0;

ДОЬНе ЕО^(Е1) Бо {проверка на конец файла Е1}

Вед±п

Кеас1(Е1_лЫ); {чтение элемента из файла Е1} ДОгл_-Ье (Р2, Ы); {запись элемента в файл Е2} 3: =3+Ы; {вычисление суммы} Еп< 1;

{запись суммы элементов в конец файла Е2}

Игл-Ъе (Е2, 5);

ДОгл.-Ье (¹ Результат находится в файле Бап2.с1а-Ь^|) С1озе(Е1); {закрытие файла Е1 для чтения} С1озе(Е2); {закрытие файла Е2 для записи} КеасИп;

Епс1.

Задания для самостоятельной работы

1. Дан файл Р, компоненты которого являются целыми числами. Найти:

а) число элементов;

б) наибольшее из значений; если их несколько, то подсчитать число таких элементов;

в) среднее арифметическое элементов.

2. Даны символьные файлы Ри С. Записать в файл Я:

а) все компоненты файлов Р и С;

б) все латинские буквы (большие и маленькие) файла Р.

3. Дан целочисленный файл А. Записать в файл В все четные числа, а в файл С все нечетные.

4. Даны два файла А и В (тип элементов одинаковый). Поменять местами содер­жимое этих файлов.

Примечание. Можно решить эту задачу двумя способами. Первый — исполь­зовать процедуру Кепаше, второй — переписать все содержимое первого файла в промежуточный, затем все содержимое второго файла в первый, а теперь вернуть все из промежуточного во второй. Для лучшей реализации второго способа можно написать процедуру, которая будет переписывать все из одного файла в другой. В этом случае в разделе типов надо описать свой тип данных для файловых пере­менных.

5. Дан символьный файл Р. Записать в перевернутом виде элементы файла Ръ файл С.

6. Даны два файла, причем первый А — целочисленный, то есть его элементы целые числа, а второй В — символьный. Вывести на экран все числа первого, а рядом с ними элементы второго с этим номером, если элемента второго файла с данным номером нет, то сообщить об этом.

Упражнение № 13. Текстовые файлы

Пример 34. Дан текстовый файл, содержащий только целые числа, в каждой строке может быть несколько чисел, которые разделяются пробелами. Вывести на экран все числа с учетом разбиения на строки и подсчитать число элементов в каждой строке.

Решение. Пусть в файле содержится следующая информация:

-32
					-5
	-8		-12
-1	-2	-4
-1	-2

 

Этот файл можно создать в среде ТигЬо Ра§са1 таким образом:

• создать новый файл (команда Ыем меню РИё)\

• записать все числа в строках через пробелы;

• сохранить его, например «а: тИ.йаЬ>.

Теперь этот файл будем использовать в программе.

Ргодгат Ехатр1е_34; Уаг Г: Тех'Ь;

х, к: 1п-Ьедег; Ведз.п

Азз: 1дп(Е, 'а: Л-П-Ы. с! ап¹); {связываем с внешним файлом}

КезеМЕ); {открываем для чтения}

ИМ1е ЫоЪ Ео^(Г) Оо {пока не конец файла}

Ведз.п

к: = 0; {начальное число элементов строки} Ш111е N0!: Ео1п(Е) Оо {пока не конец строки} Вед±п

КеасЦЕ, х); {считываем очередное число} ДОгл-Ъе (х, ^{1 1}); {вывод его на экран} 1пс(к); {увеличиваем счетчик}

Епс1;

Югл.-Ье1п (' в строке¹, к, ¹ элементов ¹); КеасИп(Е); {переходим к следующей строке файла} Епс1;

С1озе(Е); {закрываем файл} КеасИп; Епс!.

Пример 35. Дан текстовый файл, содержащий программу на языке Паскаль. Про­верить эту программу на несоответствие числа открывающих и закрывающих круг­лых скобок. Считать, что каждый оператор программы занимает не более одной строки файла.

Решение. Так как по условию задачи каждый оператор занимает не более одной строки, то будем подсчитывать число открывающих и закрывающих скобок в од­ной строке. Надо заметить, что при проверке правильности расстановки скобок в строке число рассмотренных закрывающих скобок не должно превышать числа уже рассмотренных открывающих скобок. Кроме того, такой файл должен быть создан заранее.

Ргодгат Ехатр1е_35; Уаг Е: Тех" Ь;

к1, к2, п: 1п-Ьедег; СЪ.: СЪаг;

Ъод: 1с, Рр: Воо1еап; Ведл-п

{с именем файла Е связывается внешний файл} Азз1дп(Е, ¹ а:...¹);

Кезе" Ь(Е); {открытие файла Е для чтения} п: =0; {счетчик количества строк}

Ъод1с: =Тгие; {пока ошибки не определены, то значение Тгие}

ШглПе ЫоЪ Ео^ (Е) Бо {пока не конец файла}

Вед±п

1пс(п); {увеличиваем счетчик количества строк} к1: =0; {счетчики количества открывающих скобок} к2: =0; {счетчики количества закрывающих скобок} Рр: =Еа1зе;

{Рр предназначена для определения ошибки расстановки скобок в строке, начальное значение Еа1зе, так как пока ошибки расстановки не было} ШНе N01: Ео1п (Е) Во {пока не конец текущей строки файла} Вед±п

КеасЦР, СЬ); {очередной символ строки}

{если встретили открывающую скобку, то увеличиваем их счетчик}

СЬ = '(' ТЪеп 1пс(К1); {если встречена закрывающая скобка, то если она стоит не раньше открывающей, значение К1< К2, поэтому просто уве­личиваем счетчик этих скобок, иначе помечаем Рр значени­ем Тгие}

IЁ (СЪ. = ') ') ТЬеп И (К1< К2) ТЬеп 1пс(К2) Е1зе Рр: =Тгие; Епс1;

{если не все закрывающие скобки расставлены (К1< Ж2) или одна из закрывающих скобок стоит раньше открывающей (Рр=Тгие), то была ошибка расстановки} II: (К10К2) Ог Рр ТЬеп Вед±п

ДОг11: е1п (¹ Ошибка в ¹, Ы, ¹ строке ¹); {помечаем, что в одной из строк была ошибка} Ьодл-С: =Еа1зе; Епс1;

Кеас11п(Е);

{переходим на следующую строку файла}

Епс1;

{если значение остается истинным, то ошибок расстановки, не было} И Ьод1с ТЪеп ^г11: е1п (¹ Скобки расставлены правильно¹); С1озе(Е); {закрываем файл} Кеас11п; Епс1.

Задания для самостоятельной работы

1. Дан текстовый файл, содержащий целые числа. Найти:

а) максимальный элемент в каждой строке;

б) номер данного числа; если такого нет в данной строке, то сообщить об этом.

2. Дан текстовый файл, содержащий строки. Найти:

а) число строк;

б) число строк, начинающихся и заканчивающихся одинаковыми символами;

в) самые короткие строки;

г) симметричные строки.

3. Дан текстовый файл. Вставить в начало каждой строки ее номер и записать преобразованные строки в новый файл.

4. Даны два текстовых файла. Записать в третий только те строки, которые есть и в первом, и во втором файлах.

5. Дан текстовый файл. Дописать в его конце следующие данные: число строк, число символов в каждой строке, число элементов в каждой строке.