Массивы. Упражнение № 14. Одномерные массивы

Упражнение № 14. Одномерные массивы. Заполнение массива.

Простейшие операции с массивами

Пример 36. Найти сумму пяти целых чисел.

Решение. Для решения этой задачи необходимо описать пять переменных для целых чисел и еще одну — для их суммы. Обозначим первые как а\, а!, аЪ, а4 и «5, а их сумму — 5. Тогда можно составить такую программу, используя функцию нахождения суммы пяти чисел:

Ргодгат Ехатр1е_36;

Уаг а1, а2, аЗ, а4, а5, з: 1п1: едег;

ГипсЫоп Зит (х1, х2, хЗ, х4, х5: 1п1: едег): 1п1: едег;

Вед1п

5ит: =х1+х2+хЗ+х4+х5;

Еп< 1;

Вед±п

ДОгл_1: е1п (' введите пять целых чисел¹);

КеасИп(а1, а2, аЗ, а4_уа5); {вводим пять целых чисел}

з: =5иш(а1, а2, аЗ, а4, а5); {находим их сумму}

ДОгл_1: е1п (¹ их сумма равна ^! , з); {вывод результата на экран} КеасИп;

Епс1.

А как найти сумму, например, 100 целых чисел? Здесь необходимо использо­вать массив.

Пример 37. Составить программу нахождения суммы элементов массива.

Решение. Опишем две процедуры (формирования и вывода массива) и функцию нахождения суммы элементов, которые будем использовать в основной части. За­метим, что заполнение и вывод массива можно осуществить только поэлементно, то есть можно сначала присвоить значение первому элементу, затем второму и так далее, то же самое и с выводом на экран — выводим первый, второй, третий... и так до последнего. Будем вводить значения элементов массива с клавиатуры.

Ргодгат Ехатр1е_37;

СопзЪ п=30; {п - это число элементов массива}

Туре туаггау=Аггау [ 1.. п] 01: 1п1: едег;

Уаг А: туаггау; з: 1п1: едег;

{з - значение этой переменной будет равно сумме всех элементов массива}

Ргосейиге Iпл. 1: 1 (Уаг ш: туаггау);

Уаг ±: Iпоедет;

{1 - это переменная для работы с элементами массива} Вед±п

ЭДг11: е1п ('введите \п, ¹ чисел¹); Еог 1: =1 То п Во {ввод массива с клавиатуры} КеасИп(ш[1]); {чтение 1-го элемента} Еп< 1;

Ргосейиге Рг1п1: (т: туаггау);

Уаг 1: 1п1: едег;

Вед1п

Еог 1: =1 То п Эо {вывод массива}

ЭДгИе (т[ 1 ]: 3); {вывод 1-го элемента} ДОгИ: е1п; Епс1;

Рипс*: ±оп 5ит(т: туаггау): 1п1: едег;

Уаг 1, зит: 1п1: едег;

Вед±п

зит: =0; {начальное значение суммы}

Еог л_: =1 То п Эо зит: =зит+т [ 1 ]; {к уже найденной сумме первых (1-1) элементов прибавляем 1-й элемент} Епс1; Вед±п

1п1" Ы (А); {обращение к процедуре формирования}

Рг1п1: (А); {вывод массива}

з: =5иш(А); {нахождение суммы элементов}

ДОг11: е1п (¹ их сумма равна ', з); {вывод результата на экран} КеасИп; Епй.

Первый способ задания одномерного массива — это задание с клавиатуры (он был рассмотрен в примере выше — процедура 1пН1).

Второй способ задания — это задание с помощью генератора случайных чисел; этот способ более удобен, когда много элементов в массиве.

Пример 38. Составим программу заполнения и распечатки одномерного массива с помощью генератора случайных чисел. Процедура вывода уже составлена ранее, а процедуру формирования напишем новую.

Ргодгат Ехатр1е_38; СопзЪ п=30; (1(1=51;

{п - это число элементов массива, сМ - для генератора случайных чисел} Туре туаггау = Аггау [1..п] 1п1: едег; Уаг А: туаггау;

Ргосейиге 1пИ: 2(Уаг т: туаггау);

{процедура заполнения (инициализации) массива случайными числами}

Уаг л.: 1п" Ьедег;

Вед±п

Еог 1: =1 То п Во т [ I]: =-25+Капс1от (с! с!);

{Капс1от выбирает случайное число из отрезка от 0 до сН-1, тогда 1-му элементу массива будет присвоена сумма выбранного случай­ного числа и -25, таким образом, массив будет заполняться слу­чайными числами от -25 до -25+ (сМ-1), то есть до -26+сМ}

Епс1;

Ргосес1иге Ргл_п1: (ш: туаггау); {процедура вывода (распечатки) массива} Вед±п

Капскэтхге; {включение генератора случайных чисел} 1пл_1: 2 (А); {обращение к процедуре заполнения массива} Ргл_п1: (А); {обращение к процедуре вывода заполненного массива} КеасИп; Епс1.

Третий способ задания — это чтение чисел из файла.

Пример 39. Пусть в файле записано несколько строк, а в каждой из них по 30 целых чисел. Составить программу с использованием процедуры заполнения массива из файла.

Ргодгат Ехатр1е_3 9;

Соп5" Ь п=30; {п - это число элементов массива, } Туре туаггау = Аггау [1..п] 01: 1п1: едег; Уаг А: туаггау; Е: ЬехЬ;

Ргосейиге I пл. 1: 3 (Уаг т: туаггау);

{процедура заполнения (инициализации) массива}

Уаг 1: 1п" Ьедег;

Вед±п

Рог 1: =1 То п Во Кеас1(^, т[л_]) {чтение из файла очередного числа} Еп< 1;

Ргосейиге Ргл_п1: (ш: туаггау); {процедура вывода (распечатки) массива}

Вед±п {связываем файловую переменную с конкретным внешним файлом} Азз1дп(Р, '...');

Кезе" Ь(Р); {открываем его для чтения}

ДОЪл_1е N01: Ео^(Р) Бо

Вед±п

{считываем очередную строку}

1п11: 3 (А); {обращение к процедуре заполнения массива} РГ1П1: (А); {обращение к процедуре вывода} КеасИп (Е); Еп< 1; КеасПп; Епё.

Задания для самостоятельной работы

1. Найти сумму положительных элементов массива.

2. Найти сумму всех четных элементов массива (или сумму элементов, кратных заданному числу).

3. Найти сумму всех четных элементов массива, стоящих на четных местах, то есть имеющих четные номера.

4. Найти сумму первых пяти элементов массива.

5. Найти сумму элементов с М-го по А; 2-й, где к\ и к2 вводятся с клавиатуры. Сделать проверку корректности их ввода.

6. Найти сумму элементов, больших данного числа А (А вводить с клавиатуры).

7. Найти сумму элементов, принадлежащих промежутку от А до В (А и В вводить с клавиатуры).

Примечание. В задачах 1 — 7 можно находить не только сумму, но и произведение, или проверять, что сумма первых двух цифр равна сумме последних двух цифр.

8. Найти максимальный элемент массива и его номер при условии, что все элементы различные.

9. Найти номера всех отрицательных элементов (вывести их на экран); если таких нет, то сообщить об этом.

10. Найти номера всех элементов с максимальным значением.

11. Найти минимальный элемент.

12. Найти число нечетных элементов.

13. Найти число отрицательных элементов.

14. Сколько элементов массива превосходят по модулю заданное число А?

15. Найти все элементы, кратные 3 или 5. Сколько их?

16. Есть ли в данном массиве два соседних положительных элемента? Найти номера первой (последней) пары.

17. Есть ли в данном массиве элемент, равный заданному числу? Если есть, то вывести номер одного из них.

18. Найти число четных чисел среди пяти целых чисел (без использования массива).

19. Если существует треугольник со сторонами а, Ь и с, то напечатать «ДА», в других случаях напечатать «НЕТ» (значении а, Ь и с вводить с клавиатуры).

Упражнение № 15. Методы работы с элементами одномерного массива

Пример. Заменить отрицательные элементы на противоположные по знаку.

Решение. Для этого опишем процедуру. Ей будем передавать один параметр — массив, который будет результатом ее выполнения, так как некоторые элементы могут быть заменены.

Ргосейиге ЗиЬзШаНоп! (Уаг ш: туаггау);

Уаг л_: 1п1: едег;

Ведд, п

Рог 1: =1 То п Во 1± т[1]< 0 ТЪеп т[1]: =-т[1];

Епй;

Пример. Прибавить к каждому элементу число 25.

Решение. Преобразуем предыдущую процедуру.

Ргосейиге 5иЬз1: 11: а1: 1оп2 (Уаг т: туаггау);

Уаг л_: 1п1: едег;

Вед±п

Рог л_: =1 То п Во т[л_]: =т[1] + 25;

Епй;

Пример. Если элемент четный, то прибавить к нему первый, если нечетный — прибавить последний. Первый и последний элементы не изменять.

Решение. Будем просматривать каждый элемент, кроме первого и последнего, и если он четный, то есть делится на 2 без остатка, то увеличим его на значение первого элемента, иначе — на значение последнего элемента.

Ргосейиге ЗиЬзШаНопЗ (Уаг ш: туаггау);

Уаг л.: 1п1: едег;

Вед±п

Рог 11=2 То п-1 Во

I? т [ 1 ] Мое! 2=0 ТЪеп т[з.]: =т[з.] + ш[1]

Е1зе ш[1]: =ш[1]+ш[п];

Еп< 1;

Пример. Даны два одномерных массива одинаковой размерности. Получить тре­тий массив такой же размерности, каждый элемент которого равен сумме соответ­ствующих элементов данных массивов.

Решение. Пусть даны два массива А и Д состоящие из пяти элементов. Получим из них массив С, состоящий тоже из пяти элементов, первый элемент этого мас­сива равен сумме первых элементов массивов А и В, второй — сумме вторых эле­ментов данных массивов и так далее.

/		' 2
А
В
С

 

Для решения этой задачи опишем процедуру, которой передаются три пара­метра. Первые два — это два исходных одномерных массива, третий — это одно­мерный массив той же размерности, который является результатом выполнения этой процедуры и заполняется по указанному правилу.

Ргосейиге 5ит_Аг(а, Ь: туаггау; Уаг с: туаггау);

Уаг 1: 1п" Ьедег;

Вед±п

Рог 1: =1 То п Во с[1]: =а[1]+Ъ[1];

Еп< 1;

Пример. Дан первый член арифметической прогрессии и ее разность. Найти пер­вые п членов.

Решение. Пусть а\ — это первый член прогрессии, а к — это ее разность, тогда /-й член можно найти по правилу — а[1] = 1]+А;, или я[/] = а! + & (/— 1), если / =1, то а[1] = а\. Опишем процедуру, которой передаем эти два параметра и результатом выполнения является одномерный массив. Первый элемент его равен первому члену прогрессии, второй — второму и так далее. Возьмем в качестве основной первую формулу.

Ргосейиге Ргодгезз(а1, к: 1п1: едег; Уаг а: туаггау);

Уаг л.: 1п-Ьедег;

Вед±п

а[1]: =а1;

Рог 1: =2 То п Во а[1]: =а[1-1]+к

Епс1;

Пример. Даны два одномерных массива А и В. Найти их скалярное произве­дение.

Решение. Скалярным произведением двух массивов одинаковой размерности на­зывается сумма произведений соответствующих элементов. Это можно записать так:

д[1]й[1] + а[2]Ь[2] +... + а[п~ 1]Ь[п— 1] + а[п]Ь[п], где п — это число элементов в массивах.

Тогда можно составить следующую функцию:

ГипсЫоп 5р(а, Ь: туаггау): 1опд1п1:; Уаг 1: 1п1: едег;

з: Ьопдл-пЪ; Вед±п

з: =0;

Рог 1: =1 То п Оо з: =з+а[1]*Ъ[1]; 5р: =з; Епй.

Задания для самостоятельной работы

1. Изменить знак у максимального по модулю элемента массива.

2. Заменить все четные элементы на их квадраты, а нечетные удвоить.

3. Вычесть из положительных элементов элемент с номером к1, а к отрицатель­ным прибавить элемент с номером к2, нулевые элементы оставить без изменения.

4. К четным элементам прибавить А, а из элементов с четными номерами вы­честь В.

5. Отрицательные элементы возвести в квадрат.

6. Даны два целочисленных массива, состоящие из одинакового числа элемен­тов. Получить третий массив той же размерности, каждый элемент которого равен большему из соответствующих элементов данного массива.

Например, даны два массива А и В, состоящие из пяти элементов. Получим из них массив С, состоящий тоже из пяти элементов, первый элемент этого мас­сива равен большему из первых элементов массивов А и В, второй — большему из вторых элементов данных массивов и так далее.

Таким образом, получим массив С:

/
А
В
С

 

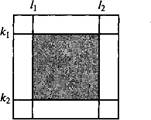
7. Дан одномерный массив А(а_ь а₂,..., а_п). Найти массив В, той же размерности В(Ь_ь Ъ_ъ..., Ь_п), где:

а) Ь_{ = а? + 2а_{— 1, для всех / = 1,..., п\

[\ (Тгие), если а, делится на к, ^ ^ [О (Раке), если не делится на к\ в) Ь; = а_х+ а₂ +... + я,, для всех / = 1,..., п.

8.Дан первый член геометрической прогрессии и ее знаменатель. Найти первые п членов этой прогрессии.

9. Получить первые п чисел Фибоначчи — первые два числа равны 1, а каждое следующее равно сумме двух предыдущих.

10.Даны два массива. Найти среднее арифметическое элементов каждого и срав­нить эти значения.

11. При выводе на экран:

а) после каждого элемента, кроме последнего, поставить точку;

б) пропустить все отрицательные.

Упражнение № 16. Удаление элементов из одномерного массива

Пример 40. Удалить из массива максимальный элемент, если все элементы разные.

Решение. Для того, чтобы решить данную задачу, необходимо:

• найти номер максимального элемента — к;

• сдвинуть все элементы, начиная с к-то, на один элемент влево;

• последнему элементу присвоить значение 0.

Ргодгат Ехатр1е_4 0; Сопз" Ь п=30; с1с1=51;

Туре туаггау = Аггау [1..п] ГпЪедег; " Уаг А: туаггау;

к: 1п" Ьедег; {к - номер максимального элемента} Ргосейиге 1п±Ъ2 (Уаг гп: туаггау);

{процедура заполнения (инициализации) массива случайными числами}

Ргосейиге Рг±пЪ1(п1: ГпЪедег; т: туаггау); {процедура вывода (распечатку) массива} Уаг л.: 1п" Ьедег; Ведхп

Еог 1: =1 То п1 Во ИгНе (ш[л.]: 5); Еп< 1;

ГипсЪ±оп Мах±тит(т: туаггау): 1п1едег;

Уаг 1, тах, тахл.: 1п" Ьедег;

Ведхп

тах: =-тах1П" Ь;

{ -тахл_п" Ь - целая константа, имеющая минимальное среди целых чисел значение, равное - 32 768 }

Еог л_: =1 То п Во {просмотр всех элементов массива} т[л_]> тах ТЬеп

{если данный элемент больше максимального элемента, найденного

среди первых 1-1 элементов, то}

Вед±п

тах: =А[л_]; {новое значение максимального элемента } тахл_: =л_; {номер максимального элемента в массиве} Еп< 1;

Мах1тит: =тах1; Еп< 1;

Ргосейиге Ве1еЪе(к1: ГпЪедег; Чаг т: туаггау); Уаг 1: 1п" Ьедег;

Вед±п {сдвиг элементов на один влево} Еог 1: =к1 То п-1 Во

ш[1]: =ш[1+1]; {1-му элементу присваиваем значение (1+1)-го} ш[п]: =0; {последний элемент равен 0} Еп< 1; Вед±п

КагкЗотхге; {включение генератора случайных чисел}

1пл.1: 2 (А); {заполнения массива А}

Ргл.п" Ы(п, А); {вывод заполненного массива А}

к: =Мах1тит(А); {поиск номера максимального элемента}

0е1е1: е(к, А); {удаление элемента с номером к}

Рг1П" Ы (п-1, А); {вывод нового массива А}

КеасИп;

Епс1.

Таким образом, на экране появятся следующие строки:

6347112 13 815 — начальный массив,

6347112815 — массив после удаления максимального элемента.

Пример 41. Предположим, что максимальный элемент встречается несколько раз.

Решение. Когда необходимо удалять несколько элементов, то это лучше всего делать с конца массива, так как иначе надо будет снова возвращаться к элементу с номером, которым только что удаляли (это возникает тогда, когда подряд идут два максимальных элемента, если первый удалим, то на его месте будет стоять снова максимальный элемент). Это можно сделать при помощи цикла с парамет­ром, который имеет следующий вид:

Гог 1: =В Оомп" Ьо А Эо < тело цикла>,

где значения переменной / будут уменьшаться на единицу, начиная от В до А (значение В должно быть меньше значения А).

Кроме того, номер максимального элемента запоминать не будем, а просмот­рим массив с конца и если элемент имеет максимальное значение, то удалим его, при этом значение счетчика к будем увеличивать на 1. Для решения этой задачи надо изменить функцию МахШит, сейчас нам нужен не номер, а значение макси­мального элемента.

Ргодгат Ехатр1е_41;

СопзЪ п=30; < 3< 3=51;

Туре туаггау = Аггау [1..п] 1п1: едег;

Уаг А: туаггау;

т, к, 1: 1п" Ьедег; {т - значение максимального элемента, к - число удаленных элементов}

Ргосес1иге 1пл_1: 2 (Уаг т: туаггау);

{процедура заполнения (инициализации) массива случайными числами}

Ргосес1иге Рг1п1: 1(п1: 1п1: едег; т: туаггау);

{процедура вывода (распечатки) массива}

ГипсЫоп Мах1тит(т: туаггау): 1п" Ьедег;.

Уаг 1, тах: 1п1: едег;

Вед±п

тах: =-тахл_п1:;

Гог л_: =1 То п Эо {просмотр всех элементов массива}

I^ т[1]> тах ТЬеп шах: =А[1];

{новое значение максимального элемента}

Махл_тит: =тах;

Епс1;

Ргосейиге Эе1е1: е(к1: 1п1: едег; Уаг ш: туаггау); {процедура удаления элемента с данным номером}

Вед±п

Капйотхге; {включение генератора случайных чисел}

1п1" Ь2 (А); {заполнение массива А}

РГ1П-Ы (п, А); {вывод заполненного массива А}

{поиск значения максимального элемента}

ш: =Мах1тит(А); к: =0;

{просмотр всех элементов, начиная с последнего} Рог л.: =п ОомпЪо 1 Эо I? А[1]=ш ТЬеп

{если данный элемент имеет максимальное значение, то}

{удаляем элемент с номером л.}

Вед±п

Эе1е1: е (л., А); 1пс(к); Епс1;

Рг1П" Ь1 (п-к, А); {вывод нового массива А} КеасИп; Епс!.

Задания для самостоятельной работы

1. Удалить первый отрицательный элемент, если такой элемент есть.

2. Удалить все отрицательные элементы.

3. Удалить все элементы, большие данного числа А (А вводить с клавиатуры).

4. Удалить все четные элементы, стоящие на нечетных местах.

5. Удалить все повторяющиеся элементы, оставив только их первые вхождения, то есть получить массив различных элементов.

6. Удалить последний четный элемент.

7. Удалить все элементы, кратные 3 или 5.

8. Удалить все элементы, начиная с /: 1-го по /: 2-й (к\ и к2 вводить с клавиату­ры). Сделать проверку корректности ввода значений к\ и к2 (к\< к2), если ввод некорректный, то вывести сообщение об ошибке и закончить работу.

Упражнение № 17. Вставка элементов в одномерный массив

Пример 42. Вставка элемента после элемента с заданным номером. Вставить чис­ло 100 после пятого элемента массива.

Решение. Пусть к — это номер элемента, после которого мы должны вставить элемент х (к их будем вводить с клавиатуры). Тогда вставка осуществляется следу­ющим образом:

• первые к элементов массива остаются без изменений;

• все элементы, начиная с (/: + 1)-го, необходимо сдвинуть на один назад;

• на место (/: + 1)-го элемента записываем значение х, то есть после к-го эле­мента массива.

Ргодгат Ехатр1е_42; СопзЪ п=10; (1(1=51;

Туре туаггау=Аггау[1.. п+1] ТпЪедег;

Уаг А: туаггау; х, к: 1п" Ьедег;

{х - вставляемое число, к - номер элемента, после которого вставляем}

Ргосес1иге 1пл_" Ь2 (Уаг ш: туаггау); {процедура заполнения (инициа­лизации) массива случайными числами}

Ргосес1иге Ргл_п1: 1(п1: 1пЪедег; т: туаггау); {процедура вывода (рас­печатки) массива}

Ргосес1иге 1пзег" Ы(к1, х1: 1п" Ьедег; Уаг ш: туаггау); Уаг 1: 1п" Ьедег;

Ведхп {сдвиг элементов на одну позицию назад} Еог л_: =п ВотяпЪо к1 + 1 Во ш[ 1+1 ]: =ш[ 1 ]; т[к1+1]: =х1; {вставка элемента на место после к1-го} Епс1; Ведхп

1п±Ь2(А);

Рг1п" Ы (п, А); { первый вывод начального массива из п элементов } Мгл-" Ье1п (^хНомер элемента, после которого вставлять, '); ЭДгл_1: е1п (^хи вставляемое число');

КеасИп (к, х); {ввод номера и вставляемого элемента} 1пзег" Ы (к, х, А);

Рг1п" Ы (п+1, А); {вывод массива после вставки в него} КеасИп; Еп< 1.

Пример 43. Вставка элемента перед данным. Вставить число 100 перед пятым элементом массива.

Решение. Эта вставка немногим отличается от предыдущей: в первой сдвигали назад все элементы, стоящие после к-то, то есть с (& +1)-го, а на его место запи­сывали новый элемент, в этой — сдвигаем все элементы с к-то, а затем на его место записываем новый.

Ргодгат Ехатр1е_4 3; СопзЪ п=10; с№=51;

Туре туаггау= Аггау [1.. п+1] 01: 1п" Ьедег; Уаг А: туаггау;

х, к: 1п" Ьедег; {х - вставляемое число к - номер элемента, после которого вставляем} Ргосес1иге 1пл_" Ь2 (Уаг ш: туаггау);

{процедура заполнения (инициализации) массива случайными числами}

Ргосес1иге Ргл.п" Ы(п1: 1п" Ьедег; т: туаггау); {процедура вывода (распечатки) массива}

Ргосес1иге 1пзег" Ь2 (к1, х1: 1п" Ьедег; Уаг ш: туаггау);

Уаг 1: 1п" Ьедег;

Ведхп

{сдвиг на одну позицию назад}

Еог л_: =п Эомп" Ьо к1 Эо т [ 1+1 ]: =т [ 1 ];

ш[к1]: =х1; {вставка х1 на место к1-го} >

Епс1;

Вед1п

1п11: 2(А);

Ргл_п1: 1 (п, А); {первый вывод начального массива} ДОгИ: е1п(¹ Номер элемента, перед которым вставлять, ')/ ДОгл_1: е1п (¹ и вставляемое число');

КеасИп(к, х); {ввод номера и вставляемого элемента} 1пзег^2(к, х, А);

РГ1П-Ы (п+1, А); {вывод массива после вставки в него} КеасИп;

Епс1.

Пример 44. Вставить число после всех элементов массива, кратных 3.

Решение. Первое, на что необходимо обратить внимание — это описание масси­ва: на сколько элементов может увеличиться массив? Максимальное число эле­ментов, после которых будет вставлен новый элемент, совпадает с числом эле­ментов массива, так как может случиться, что все элементы массива отвечают заданному свойству. Поэтому массив может увеличиться максимум в два раза.

Второе. Если мы будем просматривать элементы массива с начала и вставлять новый после элемента с заданным свойством, то номер последнего элемента каж­дый раз может меняться, кроме того, будет просматриваться и новый (вставлен­ный) элемент, который необходимо будет пропускать («перепрыгивать»), поэто­му решение будет не очень эффективным.

Лучше всего просматривать массив, начиная с конца, тогда вставляемый эле­мент мешать не будет. Кроме того, номер последнего элемента можно будет знать (если знать, сколько элементов вставлено на данный момент), при этом просмотр будет последовательным от ТУ-го до 1-го.

Ргодгат Ехатр1е_4 4;

СопзЪ п=10; сМ=51;

Туре туаггау=Аггау [ 1.. 2*п] 1п1: едег;

Уаг А: туаггау;

х, к, 1: 1п1: едег;

{х - вставляемое число, к - число вставленных элементов}

Ргосейиге 1пИ: 2(Уаг ш: туаггау);

{процедура заполнения (инициализации) массива случайными числами}

Ргосейиге Ргл_п1: 1(п1: 1п1: едег; т: туаггау);

{процедура вывода (распечатки) массива}

Ргосес1иге 1пзег1: 3(к1, х1: 1п^едег; Уаг ш: туаггау);

Уаг л.: Iпоедет;

Вед±п

{сдвиг элементов на одну позицию назад,

п+к - номер последнего элемента в данный момент}

Рог 1: =п+к ВсмпЪо к1 + 1 Во ш[1+1]: =ш[1];

т[к1+1]: =х1; {вставка элемента на место - после к1-го}

1пс(к); {увеличение счетчика вставленных элементов}

Епс1;

Вед±п

1пИ: 2 (А);

Рг1п1: 1 (п, А);

Мг11: е1п (' Введите вставляемое число');

КеасИп (х);

к: =0;

Еог л_: = п Оомп1: о 1 Оо

А [ 1 ] Мое! 3=0 ТЪеп 1пзег1: 3 (1, х, А);

Ргл_п1: 1 (п+к, А); {вывод массива после вставки в него всех элементов}

КеасИп;

Епс1.

Задания для самостоятельной работы

1. Вставить элемент после первого отрицательного элемента.

2. Вставить элемент перед последним отрицательным элементом.

3. Вставить два элемента: первый — после максимального элемента, второй — перед максимальным элементом (удобнее всего применить именно такой порядок вставки).

4. Вставить по одному элементу перед всеми элементами, кратными заданному числу.

5. Вставить по одному элементу перед всеми отрицательными элементами.

6. Вставить два элемента: первый — после всех элементов, больших данного числа Р, а второй — перед всеми элементами, большими данного числа Р (Р вводить с клавиатуры).

7. Вставить число А перед всеми элементами, большими А, а число В — после всех элементов, меньших его.

Упражнение № 18. Перестановки элементов массива

Пример. Поменять местами два элемента с номерами к\ и где к\ и к2 вводят­ся с клавиатуры.

Решение. Опишем процедуру, которой будем передавать номера переставляемых элементов и массив.

Ргоседиге 5мар(к1, к2: 1п1: едег; Уаг т: туаггау);

Уаг х: 1п1: едег;

Вед±п

х: =т[к1]; т[к1]: =т[к2]; т[к2]: =х;

Епс1;

Пример. Дан одномерный массив А, состоящий из 2п элементов. Поменять мес­тами первую и вторую его половины.

Решение. Пусть массив А состоит из 10 элементов, то есть п = 5: 1, 12, 23, 3, 7, 13, 27, 6, 9, 11. Тогда, если мы поменяем местами первую и вторую его полови­ны, то получим такой массив А: 13, 27, 6, 9, 11, 1, 12, 23, 3, 7. Заметим, что мы меняем местами элементы с номерами 1 и я+1, 2и п + 2 и так далее, последняя пара — п и 2п. Поэтому можно вывести правило перестановки — элемент с номером / меняется местами с элементом с номером п + /. Поэтому, используя процедуру 8\уар из предыдущего примера, можно в основной программе сде­лать так:

Еог л_: =1 То п Бо Змар (л_, 1+п, А);

Задания для самостоятельной работы

1. Поменять местами:

а) первый и максимальный элементы;

б) второй и минимальный;

в) первый и последний отрицательный.

2. Дан одномерный массив А, состоящий из 2п элементов. Поменять его полови­ны следующим образом: первый элемент поменять с последним, второй с пред­последним и так далее.

3.Дан одномерный массив В, состоящий из 2п элементов. Переставить его эле­менты по следующему правилу:

а) Ь[п+ 1], Ь[п + 2],..., Ь[2п], Ъ[ 1], Ъ[ 2],..., Ь[п];

б) Ь[п+1], Ь[п + 2],..., А[2/|], Ь[п], А[а2-1],..., А[1];

в) А[1], А[/| + 1], А[2], А[/|+2],..., Ь[п], Ь[2п];

г) А[2/|], Ь[2п-1],..., А[/|+1], А[1], А[2],..., Ь[п].

4. Дан одномерный массив. Переставить в обратном порядке элементы массива, расположенные между минимальным и максимальным элементами.

Упражнение № 19. Двумерные массивы. Ввод и вывод двумерного массива. Простейшие операции.

Пример 45. Составить программу ввода и вывода двумерного массива А размерно­стью 10x15.

Решение. Формирование и вывод массива описаны в виде двух процедур, кото­рые вызываются последовательно из основной программы. Надо заметить, что формирование двумерного массива можно осуществлять всеми тремя способами, описанными для одномерных массивов. Пусть в нашем примере элементы задают­ся генератором случайных чисел.

Ргодгат Ехатр1е_45; СопзЪ п=10; т=15;

Туре с! туаггау = Аггау [ 1.. п, 1..т] ОН 1пЪедег; Уаг А: с! туаггау;

Ргосес1иге 1пИ: (Уаг х: с1туаггау); {процедура формирования массива}

Уаг 1, з: 1пЪедег;

Вед±п

Еог 1: =1 То п Бо

Еог 3: = 1 То т Бо х [1_/Л: =-25+Кап< 1от (51); Епс1;

Ргосес1иге Рг1п" Ь(х: сМуаггау); {процедура вывода массива на экран}

Уаг 1, у: 1п" Ьедег;

Вед1п

Еог 1: =1 То п Бо

Вед1п {вывод 1-й строки массива}

Еог □: =1 То ш Бо Игие(х[1, ]]: 5); ДОг11: е1п; {переход на начало следующей строки} Епс1; Епс1;

Вед±п {основная программа}

1п1" Ь (А); {вызов процедуры формирования массива}

Юг1*: е1п ('Массив А: '); Рг1п1: (А) / {вызов процедуры вывода} КеасИп; Епс1.

Пример. Сформировать одномерный массив, каждый элемент которого равен сумме отрицательных элементов соответствующей строки заданной целочислен­ной матрицы.

Решение. Опишем одномерный массив, размерность которого равна количеству строк в двумерном массиве.

СопзЪ п=10; ш=15;

Туре ошуаггау=Аггау [1..п] 01: 1пЪедег;

с! туаггау=Аггау [ 1.. п, 1.. ш] 01: 1п1едег; Уаг В: ошуаггау;

А: с! туаггау; Ргосейиге Зиш(х: с! туаггау; Уаг у: ошуаггау); Уаг ^: 1п1едег; Ведхп

Рог 11=1 То п Бо Ведхп

у[1]: =0;

{задание начальных значений элементов массива суммы} Рог □: =1 То ш Бо {накопление суммы отрицательных} х[±, Л< 0 №еп у[л_]: =у[1]+х[1,; П;

Епс1; Епс1.

В основной программе обращаемся к процедуре 5ит(А, В) и остается только вывести на экран одномерный массив В, в котором записаны суммы отрицатель­ных элементов каждой строки.

Пример. Найти максимальный элемент массива и его индексы. Решение. Так как элементы могут повторяться, то договоримся, что будем запо­минать только индексы первого максимального элемента. Опишем процедуру, ко­торой передается массив, и ее результатом являются значение максимального эле­мента и индексы первой встречи такого значения.

Ргосейиге Махл_тит(х: с! туаггау; Уаг тах, тахл_, таx^: 1пЪедег);

Уаг 1, 1: 1п1: едег;

Ведхп

тах: =х[1, 1]; тахл_: =1; тахз: =1; {начальные значения} Рог л_: =1 То п Бо

Рог □: =1 То т Бо I? х[л_, Л> тах ТЬеп Ведхп {присвоение новых значений} шах: =х[1, з]; тахл_: =л_; тахз: =з; Епс1; Епс1.

Пример 46. Составить программу вычисления произведения двух квадратных цело­численных матриц А и В размером 5х 5 соответственно. Элементы результирующей, также целочисленной, матрицы С (размером 5x5) определяются по формуле

к=1

где п — размерность матриц А и В.

Решение. Формирование матриц будем производить с помощью генератора слу­чайных чисел, вычисление элементов результирующей матрицы С — с помощью вложенных циклов, где во внутреннем цикле (по параметру к) будет накапливать­ся сумма, определяющая элемент с [/, /].

Ргодгат Ехатр1е_4 6; Сопз-Ь п=5;

Туре с! туаггау=Аггау [ 1.. п, 1.. п] 1п-Ьедег; Уаг А, В, С: Ошуаггау; Ргосе< 1иге (Уаг х: Ошуаггау);

Ргосес1иге Рг1п-Ь(х: Ошуаггау);

Ргосес1иге Ми1Мх, у: Ошуаггау; Уаг т.: Ошуаггау);

Уаг к, Л 1п-Ьедег;

Вед±п

Еог 11=1 То п Во Еог ]: =1 То п Оо Ведхп

2 [л., Л: =0;

Еог к: =1 То п Во т. [ ± ^ ]: =2 [ 1 ] +х [ 1, к] *у [ к^ ]; Еп< 1; Еп< 1;

Ведхп {основная программа}

ЭДг л_-Ье1п (' массив А: '); 1пл_" Ь (А); Ргл_п" Ь (А); ЭДгл_-Ье1п ('массив В: '); 1пл_" Ь (В); Ргл_п" Ь (В); Ми1" Ь (А, В, С);

ДОгл.-Ье1п (' массив С: '); Рг1п-Ь (с); КеасИп; Епс1.

Задания для самостоятельной работы

1. Найти сумму и число элементов каждого столбца с заданным условием (хра­нить эти значения в массивах):

а) элементы, кратные к\ или к2;

б) элементы, попадающие в промежуток от А до В;

в) элементы, которые являются простыми числами;

г) данные элементы положительны и лежат выше главной диагонали.

2. Найти сумму элементов в строках с /: 1-й по к2-ю.

3. Найти номера:

а) всех максимальных элементов;

б) первых отрицательных элементов каждой строки (столбца);

в) последних отрицательных элементов каждой строки (столбца).

4. Найти число элементов в каждой строке, больших (меньших) среднего ариф­метического элементов данной строки.

5. Найти произведение двух двумерных массивов А и В, если массив А имеет размерность пхт, аВ—тхп. Определить размерность результирующего массива и правило нахождения элемента с номерами / и у.

6. Даны два квадратных массива А и В. Вывести на экран тот из них, у которого след меньше (сумма элементов главной диагонали).

7. Изменить функцию в задании 6 так, чтобы просмотр элементов заканчивался в случае, когда найден нулевой элемент.

8. Изменить функцию в задании 7 так, чтобы просмотр пар прекращался тогда, когда найдена пара неравных элементов.

9. Определить:

а) есть ли в данном массиве отрицательный элемент;

б) есть ли два одинаковых элемента;

в) есть ли данное число А среди элементов массива;

г) есть ли в заштрихованной области массива элемент, равный А (массив имеет размерность п*п):

 

 

10. Определить:

а) является ли массив логическим квадратом, то есть суммы по всем гори­зонталям, вертикалям и двум диагоналям должны быть равны;

б) добавить к предыдущему условию требование, чтобы сумма была равна данному числу А.

11. Определить, есть ли в данном массиве строка (столбец):

а) состоящая только из положительных элементов;

б) состоящая только из положительных или нулевых элементов;

в) состоящая только из элементов, больших числа А;

г) состоящая только из элементов, принадлежащих промежутку от А до В.

Упражнение № 20. Двумерный массив. Работа с элементами

Пример 47. Составить программу, запрашивающую координаты ферзя на шах­матной доске и показывающую поля доски, находящиеся «под боем».

Решение.

1. Заметим, что шахматную доску удобно представить в виде двумерного масси­ва размером 8x8. Координаты ферзя можно вводить двумя числами (номер строки и номер столбца), но в шахматах принято вводить букву и число. Буква отвечает за номер строки, а число — за номер столбца. Поэтому не будем отступать от тради­ций и введем координаты именно таким образом. В программе сделаем проверку правильности ввода и, если все правильно, переведем букву в соответствующее ей число («а» — 1, «Ь» — 2, «с» — 3, «с1» — 4, «е» — 5, «/» — 6, «§» — 7, «Л» — 8), тогда будет удобнее работать.

2. Для решения надо еще знать следующие свойства шахматной доски. Все диа­гонали делятся на восходящие и нисходящие:

 

Восходящие \       \         \       \         \       \         \       \ \       \         \       \         \       \         \       ч