Технология работы. Задача 1. Первоначальная стоимость объекта 60000 руб
Задача 1. Первоначальная стоимость объекта 60000 руб. Срок полезного использования – 2 года. Объект вводится в эксплуатацию 1 мая 2004 года. Рассчитать норму амортизации, суммы амортизационных отчислений линейным методом, накопленный износ и остаточную стоимость по месяцам. Запустите на выполнение программу Microsoft Excel, создайте рабочую книгу с именем Финансовые функции.xls. Переименуйте лист Лист1 с помощью команды меню Формат®Лист®Переименовать лист. Задайте новое имя Задача 1 Введите данные на лист Задача 1 согласно рис. 7.1 (в ячейки Е3: Е4, С7: Е18 и G7: I18 данные пока вводить не надо). E Чтобы ввести названия месяцев, в ячейку В7 введите Январь, а затем, нажав левую кнопку мыши, «протащите» курсор по ячейкам В7: В18.
При форматировании ячеек В6 и F6 воспользуйтесь командой меню Формат®Ячейки…®Граница. Выравнивание текста в этих ячейках можно произвести с помощью пробелов. В ячейку Е3 самостоятельно введите формулу для расчета нормы амортизации за один месяц. Норма амортизации рассчитывается по формуле В ячейке Е4 для расчета величины амортизационных отчислений за месяц используйте функцию АПЛ() (см. Приложение). Задайте аргументы Стоимость $Е$1, Остаток 0, Период $Е$2. В ячейку С12 введите формулу =$E$4, а в ячейку С13 введите формулу =C12+$E$4. Скопируйте формулу из ячейки С13 в ячейки С14: С18. В ячейку D7 введите формулу =C18+$E$4, а в ячейку D8 введите =D7+$E$4. Скопируйте формулу из ячейки D8 в ячейки D9: D18. В ячейки Е7: Е11 скопируйте формулы из ячеек D7: D11. В ячейки С7: С11 и Е12: Е18 введите 0. Выделите диапазон ячеек С7: Е18 и задайте денежный формат данных (кнопка Денежный формат В ячейку G11 введите формулу =$E$1–C11, а затем скопируйте эту формулу в соответствующие ячейки. Задача 2. Решить задачу 1 при условии, что используется нелинейный метод начисления амортизации. Создайте копию листа Задача 1 и переименуйте его в лист Задача 2. В ячейку Е3 введите формулу для расчета нормы амортизации. Норма амортизации при нелинейном методе рассчитывается по формуле Строку 4 можно удалить. Для расчета сумм амортизации при нелинейном методе используйте функцию ПУО(). Функция ПУО возвращает величину амортизации за один или несколько периодов, используя метод двойного процента (или иного явно указанного процента) со снижающегося остатка. Синтаксис функции ПУО(Стоимость; Остаток; Период; Нач_период; Кон_период; Коэф; Без_перекл) Аргументы Стоимость, Остаток и Период имеют тот же смысл, что и для функции АПЛ. Нач_период – это начальный период, для которого вычисляется амортизация. Кон_период – это конечный период, для которого вычисляется амортизация. Нач_период и Кон_период должны быть заданы в тех же единицах, что и период. Коэф – это коэффициент, используемый при вычислении нормы амортизации. Если Коэф опущен, то он полагается равным 2. Без_перекл – это логическое значение. Если аргумент Без_перекл имеет значение ЛОЖЬ или опущен, то Microsoft Excel переключается на линейный метод начисления амортизации, если амортизация, исчисленная по линейному методу, больше амортизации, исчисленной по нелинейному методу. Если аргумент Без_перекл имеет значение ИСТИНА, то Microsoft Excel никогда не переключается на линейный метод начисления амортизации. Введите в ячейку С11 формулу =ПУО($E$1; 0; $E$2; 0; A11-5) и скопируйте ее в ячейки С12: С17. E Обратите внимание, что пятый аргумент A11-5 в формуле В ячейку D6 введите формулу =ПУО($E$1; 0; $E$2; 0; A6+7) и скопируйте ее в ячейки D7: D17. Самостоятельно задайте формулу для ячейки Е6 и скопируйте ее в ячейки Е7: Е10. На рис. 7.2 представлена полученная таблица.
В результате можно убедиться, что, начиная с июня 2005 года, амортизация начисляется по линейному методу и составляет 1760 руб. ежемесячно. Однако, согласно Налоговому Кодексу линейный метод применяется, если остаточная стоимость достигнет 20% от первоначальной стоимости основных фондов, т.е. в нашем случае линейный метод можно применять, только начиная с декабря 2006 года. Создайте копию листа Задача 2. На новом листе необходимо запретить переключаться на линейный метод амортизации в период с июня 2005 по ноябрь 2005. Для этого необходимо исправить соответствующие формулы в ячейках D6: D17, добавив два аргумента: Коэф равный 2 и Без_перекл равный ИСТИНА. E Вместо значения ИСТИНА можно использовать значение 1. В результате в ячейке Н17 должно получиться значение 11 486 р., представляющее собой остаточную стоимость на 1 декабря 2005 года. Начиная с этого момента нужно применять линейный метод. В ячейку Е6 введите формулу =D17+$H$17/5, а ячейку Е7 формулу =E6+$H$17/5. Скопируйте последнюю формулу в ячейки Е8: Е10. Полученный результат представлен на рис. 7.3.
Задача 3. Решить задачу 1 при условии, что используется метод учета целых периодов службы основных фондов. По данному методу суммируется число периодов службы основных фонд. В нашем случае 1+2+…++24=24*(24+1)/2=300. Тогда в первом периоде амортизация равна 60000*24/300=4800 руб., во втором – 60000*23/300=4600 руб. и т.д. Для вычисления амортизации за один период служит функция АСЧ(). Синтаксис функции АСЧ(Стоимость; Остаток; Период; Текущий_период). Аргументы Стоимость, Остаток и Период имеют тот же смысл, что и для функций АПЛ и ПУО. Текущий_период – это период, для которого рассчитывается амортизация. Создайте лист Задача 3. В итоге он должен иметь вид, представленный на рис. 7.4.
В ячейку С10 введите формулу =АСЧ($E$1; 0; $E$2; A10-5), а в ячейку С11 введите формулу =C10+АСЧ($E$1; 0; $E$2; A11-5). Скопируйте формулу из ячейки С11 в ячейки С12: С16. В ячейку D5 введите формулу =C16+АСЧ($E$1; 0; $E$2; A5+7), а в ячейку D6 введите формулу =D5+АСЧ($E$1; 0; $E$2; A6+7). Скопируйте формулу из ячейки D6 в ячейки D7: D16. В ячейки Е5: Е9 формулы введите самостоятельно. Задача 4. Построить графики, отображающие изменение остаточной стоимости для всех выше рассмотренных случаях. Нажмите кнопку Мастер диаграмм ='Задача 1'! $G$11: $G$18; 'Задача 1'! $H$7: $H$18; 'Задача 1'! $I$7: $I$10; 'Задача 1'! $I$11 Чтобы добавить на диаграмму следующий ряд, соответствующий нелинейному методу, используйте кнопку Добавить. Задайте Имя Нелинейный метод. В поле Значения укажите диапазон данных ='Задача 2'! $G$10: $G$17; 'Задача 2'! $H$6: $H$17; 'Задача 2'! $I$6: $I$10 Аналогично добавьте на диаграмму ряды, соответствующие модифицированному нелинейному методу и методу учета целых периодов. Нажмите кнопку Далее. Задайте Название диаграммы Остаточная стоимость по периодам. Завершите создание диаграммы. В результате должна получиться диаграмма, представленная на рис. 7.5.
Задача 5. Рассчитать современную и будущую стоимости аннуитета за 10 лет, если величина каждого отдельного платежа 5000 руб., годовая процентная ставка 15%, платежи осуществляются в конце каждого года. Аннуитет – это тип финансовых операций, предполагающий периодический взнос денежных средств ради накопления определенной суммы в будущем. Классическим примером аннуитета являются амортизационные отчисления на воспроизводство основных фондов. Различают будущую и современную стоимость аннуитета. E Будущая стоимость аннуитета E Современная стоимость аннуитета E Если все платежи производятся в начале периода, то такой аннуитет называют пренумерандо. Если все платежи производятся в конце периода, то такой аннуитет называют постнумерандо. В данной задаче имеет место аннуитет постнумерандо. Способ 1. Введите данные согласно рис. 7.6.
Рис.7.6 E Чтобы ввести значения от 0 до 10 в ячейки В2: L2, введите 0 в ячейку В2, подведите курсор к черному квадратику в правом нижнем углу ячейки, чтобы курсор превратился в черный крестик. Нажмите и удерживайте клавишу Ctrl и, нажав левую кнопку мыши, «протащите» курсор по ячейкам C2: L2. В ячейку B4 введите формулу =1/(1+$B$1)^B2, в ячейку L5 введите формулу В ячейку В7 введите формулу =СУММПРОИЗВ(B3: L3; B4: L4). В ячейку В8 введите формулу =СУММПРОИЗВ(B3: L3; B5: L5). Недостаток данного способа – необходимо вводить все платежи. Достоинство – можно задавать различные величины платежей и ставки дисконта для каждого платежа.. Способ 2. Воспользуемся формулами для стоимости аннуитета. Современная стоимость аннуитета постнумерандо Будущая стоимость аннуитета постнумерандо Способ 3. Воспользуемся встроенными функциями Excel ПС() и БС(). В ячейку D7 вставьте финансовую функцию ПС(). В открывшемся диалоговом окне задайте аргументы: Норма В1 Кпер 10 Выплата С3 Остальные аргументы можно не задавать. Нажмите клавишу ОК. В результате в ячейке D7 окажется формула =ПС(B1; 10; C3) Синтаксис функции ПС(Норма; Кпер; Выплата; Бз; Тип) Норма – это процентная ставка дисконта (норма прибыли) за период. В случае, если, например, задана годовая ставка дисконта 18% и в течение года производятся ежемесячные платежи, то в качестве значения аргумента Норма нужно ввести 18%/12 или 1, 5% или 0, 015. Кпер – это общее число периодов выплат аннуитета. В случае, если, например, аннуитет выплачивается в течение 4 лет, платежи делаются ежемесячно, то в качестве значения аргумента Кпер нужно ввести 4*12 или 48. Выплата – это выплата, производимая в каждый период и не меняющаяся за все время аннуитета. Бз – величина дополнительного платежа, производимого в последнем периоде. Если аргумент опущен, то он полагается равным 0. Тип – это число 0 или 1. Если аргумент Тип равен 0 или опущен, то платежи осуществляются постнумерандо (в конце периода). Если аргумент Тип равен 1, то платежи осуществляются постнумерандо (в начале периода). E В финансовых функциях выплачиваемые деньги, такие как взносы в банк на накопление, представляются отрицательным числом, а полученные деньги, такие как дивиденды, представляются положительным числом. Например, взнос в банк на сумму 1 000 руб. представляется аргументом ‑ 1 000 руб. для вкладчика и представляется аргументом +1 000 руб. для банка. Самостоятельно задайте в ячейке D8 формулу для вычисления будущей стоимости аннуитета, воспользовавшись функцией БС(). Аргументы этой функции аналогичны аргументам функции ПС(), за исключением четвертого аргумента Бз, который для функции БС() обозначается Нз и равен величине дополнительного платежа, производимого в самом первом периоде. Если аргумент опущен, то он полагается равным 0. Задача 6. Инвестор предполагает накопить в течение 2 лет на счете в банке 150 тыс. руб. Платежи осуществляются в начале каждого месяца при годовой процентной ставке 10%. Рассчитать величину каждого платежа, если первоначальный взнос 30 тыс. руб. Способ 1. Финансовые функции БС(), ПС(), КПЕР(), СТАВКА(), ПЛТ() взаимосвязаны. Excel выражает каждый финансовый аргумент через другие, используя формулу
В данном случае FV =150000, PV = –30000; Тип =1, i c=10%/12; n =2*12=24. Необходимо рассчитать Р. Введите данные согласно рис. 7.7. В ячейки С5 и С7 самостоятельно введите соответствующие формулы. В ячейку Е10 введите формулу = –(C2+C8*(1+C7)^C5)*C7/((1+C7)^C5–1)/(1+C7*C9)
Способ 2. В ячейку F10 самостоятельно введите формулу, воспользовавшись функцией ПЛТ(). Задача 7. В аренду сдается здание, стоимостью 600 тыс. руб. Арендная плата выплачивается в течение 5 лет. Платежи осуществляются в конце каждого квартала. Требуемая норма прибыли 16%. Рассчитать величину каждого платежа, если арендодатель желает, чтобы к концу срока аренды современная стоимость аннуитета была равна стоимости здания. Чтобы воспользоваться рабочим листом, полученным при решении задачи 6, скопируйте его и получившийся лист назовите Задача 7. Внесите необходимые изменения в рабочий лист Задача 7 (для этого достаточно изменить исходные данные в ячейках С2: С9). В результате каждый платеж должен быть равен –20149, 05 руб. Задача 8. Инвестор предполагает накопить на счете в банке 900 тыс. руб. Планируется, что платежи в размере не более 100 тыс. руб. осуществляются в начале каждого года при годовой процентной ставке 15%. Рассчитать общее число платежей и величину каждого платежа. Создайте лист Задача 8, скопировав лист Задача 6 или Задача 7. Внесите необходимые изменения в рабочий лист согласно рис. 7.8 (для этого достаточно изменить исходные данные в ячейках С2: С9).
Способ 1. Формула для определения числа платежей имеет вид Способ 2. Воспользуемся функцией КПЕР(). В ячейку F3 введите формулу =КПЕР(C7; C10; C8; -C2; C9) Получившееся дробное значение числа платежей округлите в большую сторону в ячейке С5 с помощью функции =ОКРУГЛВВЕРХ(F3; 0). Обратите внимание, что рассчитанные в ячейках Е10 и F10 размеры платежей удовлетворяют ограничению в 100000 руб.
Задача 9. Предприятие предполагает взять кредит в размере 1500 тыс. руб. Банк предложил следующую схему платежей: ежеквартальные платежи в размере 250 тыс. руб.; платежи в конце квартала; кредит предоставляется на 2 года. Определить какую годовую норму прибыли использовал банк при расчете платежей. Способ 1. Введите данные согласно рис. 7.9.
Рис.7.9 В строку 4 формулы введите самостоятельно (см. задачу 5, рис. 7.6). В ячейку В7 формулу введите самостоятельно. Для нахождения нормы прибыли воспользуемся средством Подбор параметра (команда меню Сервис®Подбор параметра). В диалоговом окне Подбор параметра задайте данные согласно рис. 7.10.
В результате в ячейке В1 будет получена норма прибыли за квартал. Чтобы получить в ячейке В6 годовую номинальную норму прибыли нужно норму прибыли за квартал (ячейка В1) умножить на 4. Способ 2. Введите в ячейку С6 формулу =4*ВСД(B3: J3) Функция вычисляет внутреннюю доходность для ряда платежей, осуществляемых через равные промежутки времени. Синтаксис функции ВСД (Платежи; Прогноз) Платежи – диапазон ячеек, содержащих последовательность платежей. Прогноз – это величина, о которой предполагается, что она близка к результату ВСД. Задача 10. Покупатель взял в кредит 20 тыс. руб. на 12 месяцев под 25% годовых. Кредит погашается в течение года равными уплатами в конце каждого месяца. Рассчитать величину каждой уплаты, а также суммы, идущие на погашение основного долга и платежи за пользование кредитом. Уплата в погашение кредита =Платежи в погашение основного долга + Проценты на оставшуюся сумму долга. Введите данные согласно рис. 7.11. В ячейку С4 введите формулу самостоятельно. В ячейку В7 введите формулу =–ОСПЛТ($C$4; A7; $C$3; $C$1) В ячейку С7 введите формулу =–ПРПЛТ($C$4; A7; $C$3; $C$1) В ячейку D7 введите формулу =–ПЛТ($C$4; $C$3; $C$1) В ячейку Е7 введите формулу =–ОБЩДОХОД($C$4; $C$3; $C$1; $A$7; A7; 0) В ячейку F7 введите формулу =–ОБЩПЛАТ($C$4; $C$3; $C$1; $A$7; A7; 0) В ячейку G7 введите формулу самостоятельно. Скопируйте эти формулы в соответствующие ячейки.
Задача 11. Покупатель взял в кредит 20 тыс. руб. на 12 месяцев под 25% годовых. Кредит погашается в течение года уплатами в конце каждого месяца. Рассчитать величину каждой уплаты, а также суммы, идущие на погашение основного долга и платежи за пользование кредитом, если основной долг погашается равными платежами. Введите данные согласно рис. 7.12. Все необходимые формулы введите самостоятельно.
E. Для расчета выплат процентов в данной схеме погашения кредита (столбец С) может использоваться функция ПРОЦПЛАТ(). Например, в ячейку С7 можно задать функцию =ПРОЦПЛАТ($C$4; A7-1; $C$3; $C$1) Задача 12. Решить задачу 11 при условии, что кредит был взят 10 декабря 2003 года. Платежи в банк должны поступать с периодичностью один месяц. Если дата платежа приходится на праздничный или выходной день, то дата платежа переносится на первый рабочий день, следующий за нерабочим днем. Долг погашается равными платежами. Ожидаемый результат работы представлен на рис. 7.13.
Чтобы найти дату предстоящего платежа воспользуемся функцией ДАТАМЕС(). Эта функция возвращает в числовом формате дату, отстоящую на заданное количество месяцев вперед или назад от заданной даты (Нач_дата). Функция ДАТАМЕС() используется для вычисления даты платежа, приходящейся на тот же день месяца, что и дата получения кредита. Синтаксис функции ДАТАМЕС(Нач_дата; Число_месяцев) Нач_дата – это начальная дата. Число_месяцев – это количество месяцев до или после даты Нач_дата. Например, если в ячейку В7 ввести формулу =ДАТАМЕС($C$4; A7), то в результате получим дату 10.01.04. Однако этот день приходится на нерабочий день – субботу. Чтобы определить ближайший рабочий день, используют функцию РАБДЕНЬ(). E Подробности об использовании функции РАБДЕНЬ() приведены в описании лабораторной работы №5. Таким образом, чтобы найти ближайший рабочий день для даты 10.01.04 можно было бы ввести в ячейку В7 формулу =РАБДЕНЬ(ДАТАМЕС($C$4; A7); 0; $G$7: $G$14) Однако в итоге все равно получаем ту же дату 10.01.04. Это связано с тем, что значение параметра Количество_дней не должно быть равным нулю. Чтобы «обмануть» функцию РАБДЕНЬ() необходимо немного изменить формулу в ячейке В7, отняв от Нач_дата один день и задав параметр Количество_дней равным 1. =РАБДЕНЬ(ДАТАМЕС($C$4; A7)-1; 1; $G$7: $G$14) Скопируйте полученную формулу в соответствующие ячейки. Для вычисления суммы выплачиваемых процентов обычно используют формулу
Тогда в ячейку D7 необходимо ввести формулу =C1*$C$2/365*(B7-C4), а в ячейку D8 введите формулу =($C$1-СУММ(C$7: C7))*$C$2/365*(B8-B7) Последнюю формулу необходимо скопировать в ячейки D9: D18. Лабораторная работа №8 Цель. Изучить некоторые финансовые функции Microsoft Excel, связанные с анализом рынка ценных бумаг.
|

 Рис. 7.1
Рис. 7.1 , где n – срок полезного использования в месяцах.
, где n – срок полезного использования в месяцах. ).
). .
. Рис. 7.2
Рис. 7.2 Рис. 7.3
Рис. 7.3 Рис. 7.4
Рис. 7.4 и выберите тип диаграммы График. Нажмите кнопку Далее. В следующем окне щелкните по вкладке Ряд. Щелкните по кнопке Добавить и введите Имя Линейный метод. В поле Значения укажите диапазон данных
и выберите тип диаграммы График. Нажмите кнопку Далее. В следующем окне щелкните по вкладке Ряд. Щелкните по кнопке Добавить и введите Имя Линейный метод. В поле Значения укажите диапазон данных Рис.7.5
Рис.7.5 , где n – общее число платежей (периодов); Pt – платеж, произведенный в начале или конце t-ого периода (зачастую рассматривают одинаковые размеры платежей, т.е. Рt=Р); ic – доходность платежей (ставка дисконта); b t – коэффициент наращивания.
, где n – общее число платежей (периодов); Pt – платеж, произведенный в начале или конце t-ого периода (зачастую рассматривают одинаковые размеры платежей, т.е. Рt=Р); ic – доходность платежей (ставка дисконта); b t – коэффициент наращивания. , где a t – коэффициент дисконтирования.
, где a t – коэффициент дисконтирования.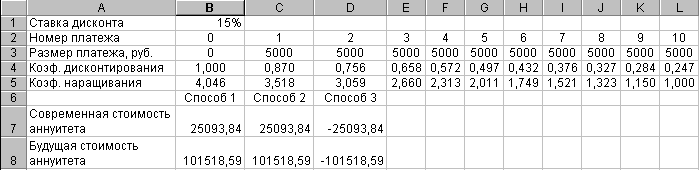
 , где Р – размер платежа. В ячейку С7 введите формулу =C3*(1-1/(1+B1)^10)/B1.
, где Р – размер платежа. В ячейку С7 введите формулу =C3*(1-1/(1+B1)^10)/B1.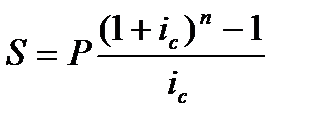 . Самостоятельно введите соответствующую формулу в ячейку С8.
. Самостоятельно введите соответствующую формулу в ячейку С8. , где PV – стоимость вклада в самом первом периоде; FV – стоимость вклада в самом последнем периоде.
, где PV – стоимость вклада в самом первом периоде; FV – стоимость вклада в самом последнем периоде. Рис. 7.7
Рис. 7.7 Рис. 7.8
Рис. 7.8 . Формула получена при условии, что PV =0. Введите в ячейку Е3 соответствующую формулу. Предварительный размер платежа Р возьмите из ячейки С10.
. Формула получена при условии, что PV =0. Введите в ячейку Е3 соответствующую формулу. Предварительный размер платежа Р возьмите из ячейки С10.
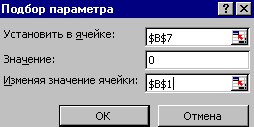 Рис. 7.10
Рис. 7.10 Рис. 7.11
Рис. 7.11 Рис. 7.12
Рис. 7.12 Рис. 7.13
Рис. 7.13



