МЕЖДУ ПУНКТАМИ
Известно, что на мелкомасштабных географических картах из-за перехода от поверхности земного эллипсоида к плоскости неизбежны искажения длин линий, исключая отдельные направления, совпадающие с линией сечения поверхности эллипсоида и поверхности вспомогательных фигур (плоскости, конуса, цилиндра), используемых для проектирования. Непосредственное измерение расстояний по прямой на мелкомасштабных картах может привести к большим ошибкам, т. к. кратчайшее расстояние будет иметь вид кривой линии. Кратчайшая линия на поверхности земного эллипсоида, представляющая собой дугу большого круга, называется ортодромией. Представить ее можно следующим образом. Если взять на глобусе две точки, удаленные друг от друга, а затем между ними натянуть нитку, то она ляжет по ортодромии. Нетрудно при этом заметить, что ортодромия будет пересекать меридианы под разными углами. Следовательно, азимуты ортодромии в разных ее точках будут различны. Сама же ортодромия на всех картах будет изображаться кривой, исключая отдельные направления (прямолинейные меридианы и экватор). Линия на поверхности земного эллипсоида, пересекающая все меридианы под одним и тем же углом, называется локсодромией, и в общем случае она изображается спиралевидной кривой. Эта линия имеет большое значение для мореплавания, т. к. движение судна на каждом участке своего пути в открытом море обычно контролируется при помощи компаса. Имеется замечательная проекция — нормальная цилиндрическая равноугольная проекция Меркатора, которая до сих пор используется для навигационных карт. Локсодромия на этих картах изображается прямой линией. Кратчайшее расстояние, т. е. расстояние по ортодромии, можно вычислять по географическим координатам пунктов, используя следующие формулы: sinS0 =sin B 1 + sin B 2 +cos B 1 – cos B 2 · cos(L2 – L1); (1)
где B1 и B2- географическая широта начального и конечного пунктов; L 1 и L 2 - географическая долгота начального и конечного пунктов; R - средний радиус кривизны земного эллипсоида. Из приведенных формул видно, что для вычисления кратчайшего расстояния необходимо определить географические координаты начального и конечного пунктов.
|

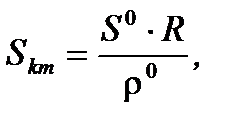 (2)
(2)


