Аналитический расчет характеристик системы
При § коэффициент загрузки сервера: ρ = λ /µ; вероятности состояний сервера (состояние определяется числом заявок в системе): § Вероятность простоя системы: P 0 § Вероятности других состояний системы: P 1 = ρ P 0; P 2 = ρ 2 P 0; P 3 = ρ 3 P 0; … Pm = ρ m P 0; Pm +1 = ρ m +1 P 0.
§ Вероятность потерь:
§ Относительная пропускная способность (доля обслуженных заявок):
§ Абсолютная пропускная способность: А = λ q – интенсивность потока обслуженных заявок. § Среднее число заявок в очереди
§ Среднее число заявок на обслуживании:
§ Среднее число заявок в системе (в очереди и на обслуживании):
§ Среднее время ожидания в очереди:
§ Среднее время пребывания заявки в системе:
3.3.2 Программа модели системы М/М/1/m Требуется смоделировать в течение 1 часа работу простейшей одноканальной СМО с ограничением на длину очереди – обработку сервером поступающих на него запросов при ограниченной буферной памяти. Поток заявок распределен по закону Пуассона с интенсивностью λ = 1.2 заявок в секунду, время обработки заявки сервером распределено экспоненциально с интенсивностью µ = 2 заявок в секунду, допустимая длина очереди m = 3. В программе модели должны определяться такие же характеристики системы, что и при аналитических расчетах. Частичное решение поставленной задачи приведено в программе 2 (все необходимые пояснения приведены в тексте программы). Задание. Дополните программу так, чтобы определялись остальные характеристики системы.
|
можно определить следующие характеристики системы:
= (1 – ρ)/(1 – ρ m +2).
.
, ρ < > 1.
.
:
.
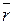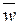= (ρ – ρ m +2)/(1 – ρ m +2).
.
.
