K_ EQU 5; коэффициент, введенный для уменьшения r_мах

L_ EQU 1.2; лямбда

MU_ EQU 2#K_; мю новое

*

* Основной сегмент

GENERATE (Exponential(1, 0, (1/L_))); Генерация заявок

* с интенсивностью L_ заявок в секунду

QUEUE SERV; Встаем в очередь. Если сервер свободен,

SEIZE SERV; то занимаем его

DEPART SERV; и освобождаем место в очереди

ADVANCE (Exponential(1, 0, (1/MU_))); обрабатываем заявку

RELEASE SERV; после обработки заявки освобождаем сервер

TERMINATE; и удаляем обработанную заявку

POTERI SAVEVALUE POTER+, 1; Добавляем 1 к потерям и

TERMINATE; удаляем потерянную заявку

*

* Сегмент задания времени моделирования и вычислений

GENERATE 3600; Задаем время моделирования - один час

TERMINATE 1; Стандартное окончание

START 1; времени моделирования

 

При прогоне программы получаем r_мах = 4, поэтому в системе будет 6 состояний S0, S1, S2, S3, S4, S5, вероятности которых можно определить аналитически по формулам, приведенным выше, а при имитационном моделировании так, как это было показано в программе 2.

Порядок выполнения работы

1. Изучить описание лабораторной работы.

2. выбрать параметры систем в соответствии с вашим номером в списке группы.

3. Определить возможные состояния систем:

– с отказами,

– с ограниченной очередью,

– без потерь.

Построить размеченные графы систем и составить системы дифференциальных и алгебраических уравнений. (Для системы без потерь строить граф и составлять системы уравнения после определения максимальной длины очереди.)

4. Решить системы дифференциальных уравнений средствами GPSS World и получить графики изменения вероятностей состояний систем.

5. определить по аналитическим формулам характеристики систем:

– с отказами,

– с ограниченной очередью,

– без потерь.

6. разработать имитационные модели систем в среде GPSS World (ограниченную очередь имитировать объектом STORAGE).

7. провести по 3 эксперимента с разработанными моделями в течение k ₁, k ₂, k ₃ часов и определить характеристики систем (k _i – определите экспериментально).

8. внести полученные данные в таблицы и оценить величины отклонений характеристик систем, полученных по имитационным моделям, интегрированием и аналитическими расчетами для каждого типа системы.

9. сделать выводы о результатах работы и подготовить отчет, содержащий все расчеты, тексты программ моделей, выдержки из стандартных отчетов и анализ полученных данных.

Вопросы для самоконтроля

1. Чем различаются одноканальные системы с отказами, с ограниченной очередью и без потерь? Как это проявляется на характеристиках систем?

2. Как реализуются различия систем п.1 в имитационных моделях?

3. Сформулируйте правила определения состояний системы (признак различия состояний).

4. Сформулируйте правила построения графа переходов системы.

5. Сформулируйте правила получения систем дифференциальных и алгебраических уравнений, описывающих поведение СМО.

6. Какие режимы работы существуют у СМО? Какова длительность переходного режима?

7. Решение системы дифференциальных уравнений? Что получаем в стандартном отчете?

8. Как использовать результаты интегрирования для получения характеристик системы: Ротк, q, A, , ?

9. Как получить графики вероятностей при решении системы дифференциальных уравнений?

10. Чему равно среднее значение интервала времени между заявками?

11. Чему равно среднее время обслуживания заявок?

12. Как определить среднее время нахождения заявки в системе (среднее время отклика системы)?

 

 

3.7 Варианты заданий
Группа 1		Группа 2
№	λ	µ	m		№	λ	µ	m
	2.15	2.45				5.78	5.99
	1.24	1.48				4.12	4.69
	3.56	4.01				5.60	6.11
	3.22	3.25				1.25	1.65
	2.98	3.15				1.57	1.88
	5.15	5.67				2.45	2.76
	3.66	3.98				5.65	5.73
	5.32	5.65				8.04	8.21
	1.25	1.34				3.18	3.32
	2.16	2.50				6.21	6.84
	4.40	4.69				1.96	2.43
	2.75	2.96				3.65	4.01
	3.12	3.43				4.12	4.36
	0.86	0.91				5.12	5.43
	7.45	7.51				3.25	3.51
	5.11	5.28				1.76	1.89
	6.08	6.22				2.35	2.73
	7.44	7.74				6.34	6.74
	1.93	2.05				4.56	4.98
	4.00	4.21				4.14	4.56
	3.28	3.53				5.23	5.47
	4.12	4.39				4.25	5.43
	3.19	3.35				2.98	3.31
	0.46	0.50				6.10	6.75
	2.52	2.86				0.98	1.22
	2.60	2.75				1.86	1.90
	4.23	4.90				2.50	2.73
	2.50	2.60				4.24	4.50
	3.22	3.53				5.30	5.72
	0.86	1.10				4.50	5.49

 

Указание: Для уменьшения максимальной длины очереди в системе без потерь в качестве интенсивности обслуживания принять ,

где k = 5…10 так, чтобы максимальное значение очереди было порядка 2…5.

 

4 Лабораторная работа №4. Моделирование многоканальных смо
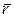