Стационарный режим
Стационарный режим существует, если для одноканальной системы: В стационарном режиме производные равны 0 (вероятности имеют постоянные значения), поэтому система дифференциальных уравнений превращается в систему линейных алгебраических уравнений Литтла – λ P 0 + µ P 1 = 0, (1) λ P 0 – µ P 1 = 0, к которым надо добавить уравнение нормировки P 0 + P 1 = 1. (2) Решая эту систему, находим значения вероятностей в стационарном режиме. Из (1) получаем Подставив P 1 в (2), получаем Откуда
С учетом (2')
Для параметров примера получаем P 0 = 0.625; P 1 = 0.375. Эти значения вероятностей совпадают со значениями, полученными интегрированием. Относительная пропускная способность (доля обслуженных заявок)
Абсолютная пропускная способность (интенсивность обслуженных заявок) A = 3.2.2 Программа модели системы М/М/1/0 Пусть требуется смоделировать в течение 1 часа работу простейшей одноканальной СМО с отказами – обработку сервером поступающих на него запросов при отсутствии буферной памяти. Поток заявок распределен по закону Пуассона с интенсивностью λ = 1.2 заявок в секунду, время обработки заявки сервером распределено экспоненциально с интенсивностью µ = 2 заявок в секунду. В программе модели должны определяться такие же характеристики системы, что и при аналитических расчетах, но не по аналитическим формулам, а путем подсчета различных событий. Некоторые характеристики выдаются в Стандартном отчете GPSS. Частичное решение этой задачи приведено в программе 1 (все необходимые пояснения приведены в тексте программы). Задание. Дополните программу блоками SAVEVALUE для определения относительной и абсолютной пропускной способности (q и A) системы.
|

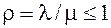 . если
. если  > 1, то стационарного режима нет.
> 1, то стационарного режима нет.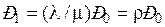 .
. .
.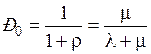 .. (2’)
.. (2’) .
. =0.625.
=0.625.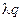 = 1.2 . 0.625 = 0.75.
= 1.2 . 0.625 = 0.75.


